
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�����ABCD�ı�AD��x���ϣ���A��ԭ�㣬AB=3��AD=6����������ÿ��2����λ������x���������������˶���ͬʱ��P��A�������ÿ��1����λ������A��B��C��D��·���������˶�����P���˶���D��ʱֹͣ�˶�������ABCDҲ��ֹ֮ͣ�˶���
��1����P���A���˶���D�������ʱ�䣻
��2����P����˶�ʱ��Ϊt���룩��
�ٵ�t=8ʱ�������P�����ꣻ
������OAP���ΪS����̽����P���˶�������S��t֮��Ĺ�ϵʽ��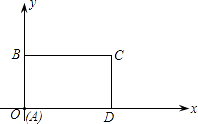
���𰸡�
��1��
�⣺P���A���˶���D�������ʱ��=��3+6+3����1=12���룩
��2��
�⣺�ٵ�t=8ʱ��P���A���˶�����BC�ϣ�
��ͼ��

����P��PE��AD�ڵ�E��
��ʱA�㵽E���ʱ��=8�룬AB+BP=8��
��BP=5����PE=AB=3��AE=BP=5
�߾��������ƶ�2��8=16
��OE=OA+AE=16+5=21
���P��������21��3����
�ڷ����������
��0��t��3ʱ����P��AB���˶�����ʱOA=2t��AP=t
��s= ![]() ��2t��t=t2
��2t��t=t2
��3��t��9ʱ����P��BC���˶�����ʱOA=2t
��s= ![]() ��2t��3=3t
��2t��3=3t
��9��t��12ʱ����P��CD���˶�����ʱOA=2t��AB+BC+CP=t
��DP=��AB+BC+CD������AB+BC+CP��=12��t
��s= ![]() ��2t����12��t��=��t2+12t����������s��t֮��ĺ�����ϵʽ�ǣ�s=
��2t����12��t��=��t2+12t����������s��t֮��ĺ�����ϵʽ�ǣ�s= 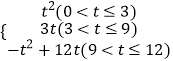
����������1�����AB+BC+CD���ɵó����ۣ���2�������жϳ���P�ڱ�BC�ϣ������ƶ��ĵ�λ������ȷ������������ƽ�Ƶĵ�λ�����ɵó����ۣ��ڷ�����������������ε������ʽ������⣮
�����㾫�������ڱ��⿼���ƽ���ı��ε��ж������ʣ���Ҫ�˽���һֱ�߹�ƽ���ı������Խ��ߵĽ��㣬������ֱ�߱�һ��Ա߽��µ��߶��ԶԽ��ߵĽ���Ϊ�е㣬����������ֱ�߶��ȷִ�ƽ���ı��ε�������ܵó���ȷ�𰸣�


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,������OABC����ƽ��ֱ������ϵ��,��A,C�ֱ���x,y�����������,��֪��B(4,2),������OABC����,ʹ�õ�C�Ķ�Ӧ��Pǡ�������߶�OA(�����˵�O,A)��,�ۺ�����ֱ�߷ֱ�BC��OA�ڵ�D��E������P���߶�OA���˶�ʱ,����P��OA�Ĵ��߽��ۺ�����ֱ���ڵ�Q.
��1����֤��CQ=QP
��2�����Q������Ϊ(x,y),��y����x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ;
��3����ͼ2,����OQ,OB,����P���߶�OA���˶�ʱ,��������OBQ�����ΪS,��xȡ��ֵʱ,Sȡ����Сֵ,�������Сֵ��
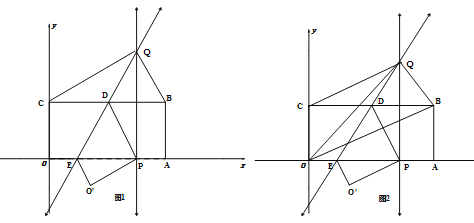
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ����ƽ���ʽ������ǣ� ��
A.��2a+b��(2b-a)
B.( ![]() x+1)(-
x+1)(- ![]() -1)
-1)
C.(3x-y)(-3x+y)
D.(-x-y)(-x+y)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬʱ�������ʵؾ��ȵ����ӣ��۲�����һ��ĵ������������ӵĵ�����ͬ�ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������������a��b������x��y�Ķ�Ԫһ�η��̣�a��b��x����a+b��y=a+b��һ�鹫���⣬����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB��8cm��BC��10cm���۵����ε�һ��AD �� ʹ��D����BC�ߵ��е�F�����ۺ�ΪAE �� ��CE�ij���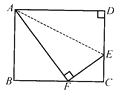
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ؿ�����ij���ӵ�·�峧������ɽ��ѧ��2014��Ӧ���ҵ������Ƹ��˾ְԱ����ӦƸ�ߵ�רҵ֪ʶ��Ӣ��ˮƽ���μ����ʵ�������Ż��������в��Ի�ɹ��϶�������ĵ÷����ֶ�Ϊ100�֣�����ķ����ֱ�5��3��2�ı�������ÿ�˵�����ܷ֣���4λӦƸ�ߵĵ÷������
�÷� | רҵ֪ʶ | Ӣ��ˮƽ | �μ����ʵ���� |
�� | 85 | 85 | 90 |
�� | 85 | 85 | 70 |
�� | 80 | 90 | 70 |
�� | 90 | 90 | 50 |
��1���ֱ����4λӦƸ�ߵ��ܷ֣�
��2���������ˡ�רҵ֪ʶ����ƽ����Ϊ85�֣�����Ϊ12.5�����ˡ�Ӣ��ˮƽ����ƽ����Ϊ87.5�֣�����Ϊ6.25������������ˡ��μ����ʵ�������Ż�ȡ���ƽ���ּ����
��3��������1���ͣ�2���е��й����ݣ���Դ�ѧ��ӦƸ���кν��飿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com