
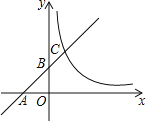
【题目】如图,![]() (b为常数)的图象与x轴,y轴分别交于点A,B与反比例函数
(b为常数)的图象与x轴,y轴分别交于点A,B与反比例函数![]() (x>0)的图象交于点C.若ACBC=4,则k的值为_____.
(x>0)的图象交于点C.若ACBC=4,则k的值为_____.
【答案】2
【解析】
作CD⊥x轴于D,先求出y=x+b(b为常数)的图象与x轴,y轴分别交于点A,B两点坐标,根据勾股定理得出AB,再根据C(x,x+b),△ADC也是等腰直角三角形,求出AC, 再根据ACBC=4,得出x(x+b)的值即可.
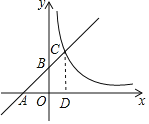
解:作CD⊥x轴于D,则OB∥CD,ADC=90,
∵y=x+b(b为常数)的图象与x轴,y轴分别交于点A,B,
∴A(-b,0),B(0,b),
∴OA=OB=b,∴AB=![]() b;
b;
∵△AOB是等腰直角三角形,OB∥CD,
∴△ADC也是等腰直角三角形,
∴AD=CD,∴C(x,x+b),
∴k=x(x+b),且AC=![]() (x+b)
(x+b)
∵ACBC=4,∴![]() (x+b)
(x+b)![]() b=4;
b=4;
∴x(x+b)=2 ∴k=2
故答案为2.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,半径为1的
中,半径为1的![]() 与
与![]() 轴正半轴和
轴正半轴和![]() 轴正半轴分别交于
轴正半轴分别交于![]() 两点,直线
两点,直线![]() :
:![]() 与
与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点.
两点.

(l)当直线![]() 与
与![]() 相切时,求出点
相切时,求出点![]() 的坐标和点
的坐标和点![]() 的坐标;
的坐标;
(2)如图2,当点![]() 在线段
在线段![]() 上时,直线
上时,直线![]() 与
与![]() 交于
交于![]() 两点(点
两点(点![]() 在点
在点![]() 的上方),过点
的上方),过点![]() 作
作![]() 轴,与
轴,与![]() 交于另一点
交于另一点![]() ,连结
,连结![]() 交
交![]() 轴于点
轴于点![]() .
.
①如图3,若点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长并写出解答过程;
的长并写出解答过程;
②如图2,若点![]() 与点
与点![]() 不重合时,
不重合时,![]() 的长是否发生变化,若不发生变化,请求出
的长是否发生变化,若不发生变化,请求出![]() 的长并写出解答过程;若发生变化,请说明理由.
的长并写出解答过程;若发生变化,请说明理由.
(3)如图4,在(2)的基础上,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() ,若点
,若点![]() 在
在![]() 的延长线时,请用等式直接表示线段
的延长线时,请用等式直接表示线段![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN恰好重合,其量角器最外缘的读数是从N点开始(即N点的读数为0°),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.
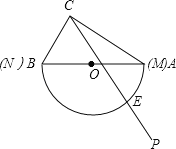
(1)当旋转7.5秒时,连接BE,试说明:BE=CE;
(2)填空:①当射线CP经过△ABC的外心时,点E处的读数是 .
②当射线CP经过△ABC的内心时,点E处的读数是 ;
③设旋转x秒后,E点出的读数为y度,则y与x的函数式是y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
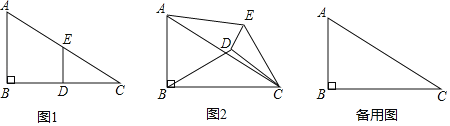
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题解决:(1)①当α=0°时,![]() = ;②当α=180°时,
= ;②当α=180°时,![]() = .
= .
(2)试判断:当0°≤a<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
问题再探:(3)当△EDC旋转至A,D,E三点共线时,求得线段BD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植![]() 、
、![]() 两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了
两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.设该基地种植了![]() 种核桃
种核桃![]() 亩.
亩.
(Ⅰ)若该基地收获两种核桃的年总产量为25 800千克,则![]() 、
、![]() 两种核桃各种植了多少亩?
两种核桃各种植了多少亩?
(Ⅱ)全部收购后,总收入为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式.若要求种植
之间的函数关系式.若要求种植![]() 种核桃的面积不少于
种核桃的面积不少于![]() 种核桃的一半,那么种植
种核桃的一半,那么种植![]() 种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
种核桃多少亩时,该种植基地的总收入最多?最多是多少元?
解:(Ⅰ)先用含![]() 的代数式填空,再完成解答.
的代数式填空,再完成解答.
由种植了![]() 种核桃
种核桃![]() 亩,可知
亩,可知![]() 种核桃种植的亩数为________,则
种核桃种植的亩数为________,则![]() 种核桃的年总产量为________千克,
种核桃的年总产量为________千克,![]() 种核桃的年总产量为________千克.
种核桃的年总产量为________千克.
根据题意列出方程________________________;
解得:
(Ⅱ)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
(1)慢车的速度为_____km/h,快车的速度为_____km/h;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500km.

查看答案和解析>>
科目:初中数学 来源: 题型:
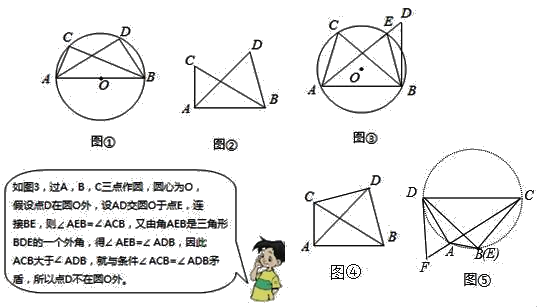
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是边BC的中点,连接AE并延长,交DC的延长线于点F,连接AC,BF.
(1)求证:△ABE≌△FCE;
(2)当四边形ABFC是矩形时,当∠AEC=80°,求∠D的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com