
【题目】阅读下面材料:在数学课上,老师给同学们布置了一道尺规作图题: 尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.已知:如图1,正比例函数和反比例函数的
图象分别交于M、N两点.
要求:在y轴上求作点P,使得∠MPN为直角.
小丽的作法如下:如图2,以点O为圆心,以OM长为半径作⊙O,
⊙O与y轴交于P1、P2两点,则点P1、P2即为所求.
老师说:“小丽的作法正确.”
请回答:小丽这样作图的依据是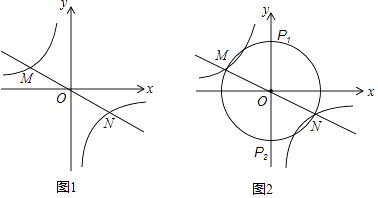
科目:初中数学 来源: 题型:
【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1: ![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q是反比例函数y= ![]() 图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s). 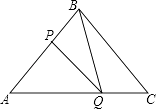
(1)当x为何值时,PQ∥BC;
(2)当△APQ与△CQB相似时,AP的长为;
(3)当S△BCQ:S△ABC=1:3,求S△APQ:S△ABQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.求所组成的两位数是5的倍数的概率.(请用“画树状图”或“列表”的方法写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: “怀山俊秀,柔水有情”﹣怀柔,一直受到世人的青睐.早在上世纪90年代,联合国第4届世界妇女大会NGO论坛的举办使怀柔蜚声海内外,此后,随着世界养生大会、国际青少年嘉年华、全国汽车拉力赛等一系列活动赛事的成功举办,为这座国际交往新城聚集了庞大的人气.2014年11月11日,全世界的眼光再次聚焦在北京怀柔雁栖湖,这里成功举办了第22次APEC领导人峰会.现如今怀柔已成为以自然风光游为基础,休闲度假游、乡村美食游、满族风情游为特色,影视文化游、健身养生游、竞技赛事游为时尚的多元化旅游胜地.
随着怀柔旅游业的迅速发展,也带动了怀柔的经济收入.据统计,2011年全年接待游客1047万人次,比上一年增长5.3%;2012年全年接待游客1085万人次,比上一年增长3.7%; 2013年全年接待游客1107.6万人次,比上一年增长2%; 2014年全年接待游客1135万人次,比上一年增长2.4%;2015年全年接待游客1297.4万人次,比上一年增长14.3%.(以上数据来源于怀柔信息网)根据以上材料解答下列问题:
(1)用折线图将2011﹣2015年怀柔区全年接待游客量表示出来,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估 2016年怀柔区全年接待游览客量约万人次,你的预估理由是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )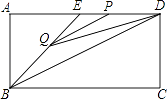
A.
B.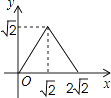
C.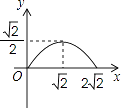
D.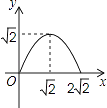
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于点C,连接AC,BC.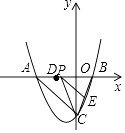
(1)求该抛物线的解析式;
(2)若点P是x轴上的一动点,且位于AB之间,过点P作PE∥AC,交BC于E,连接CP,设P点横坐标为x,△PCE的面积为S,请求出S关于x的解析式,并求△PCE面积的最大值;
(3)点为D(﹣2,0),若点M是线段AC上一动点,是否存在M点,能使△OMD是等腰三角形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com