练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在四边形ABCD中，AB∥CD，AD//BC，点E，F在对角线AC上，且AE=CF，请你分别以E，F为一端点，和图中已标字母的某点连成两条相等的新线段（只需证明一组线段相等即可）.

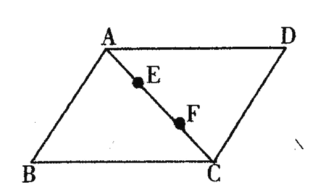
    （1）连接 ；

    （2）结论： = ；

    （3）证明：

    【答案】（1）BE，DF；（2）BE，DF；（3）见解析

    【解析】

    此题的答案不唯一．可以连接BE，DF，根据平行四边形的性质和已知条件证明全等三角形，从而证明BE=DF.

    解：（1）连接BE，DF；

    （2）结论：BE=DF；

    （3）证明：连接BE，DF，如图所示：


    ∵在四边形ABCD中，AB∥CD，AD∥BC，
    ∴AB=CD，∠BAE=∠DCF，
    又∵AE=CF，
    ∴△ABE≌△CDF．
    ∴BE=DF．

    故答案为：（1）BE，DF；（2）BE，DF.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】二次函数的图象如图所示，则下列关系正确的是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，每个小正方形边长都是1．

    （1）按要求作图： △ABC关于轴对称的图形△；

    （2）将点先向上平移个单位，再向右平移个单位得到点的坐标为 ；

    （3）△的面积为 ；

    （4）若为轴上一点，连接 ，则△周长的最小值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：等腰三角形OAB在直角坐标系中的位置如图，点A的坐标为（-3,3），点B的坐标为（﹣6，0）．

    （1）若三角形OAB关于y轴的轴对称图形是三角形OA′B′，请直接写出A、B的对称点A′、B′的坐标；

    （2）若将三角形OAB沿x轴向右平移a个单位，此时点A恰好落在反比例函数y=的图象上，求a的值；

    （3）若三角形OAB绕点O按逆时针方向旋转α度（0＜α＜90）．

    ①当α=30°时点B恰好落在反比例函数y=的图象上，求k的值；

    ②问点A、B能否同时落在①中的反比例函数的图象上，若能，求出α的值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知的直径，延长到，使，过作的切线，为切点，连接、．求：

    的长；

    的值；

    的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一般情况下，不成立，但有些数可以使得它成立，例如：a＝1，b＝2．我们称使得成立的一对数a，b为“相伴数对”，记为（a，b）．

    （1）判断数对（﹣2，1），（3，3）是否是“相伴数对”；

    （2）若（k，﹣1）是“相伴数对”，求k的值；

    （3）若（4，m）是“相伴数对”，求代数式的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE.

    （1）求证：CE＝AD；

    （2）当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

    （3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某一出租车一天下午以鼓楼为出发地在东西方向运营，向东走为正，向西走为负，行车里程（单位：㎞）依先后次序记录如下：+9，-3，-5，+4，-8，+6，-3，-6，-4，+10.

    ⑴将最后一名乘客送到目的地，出租车离鼓楼出发点多远？在鼓楼的什么方向？

    ⑵若每千米的价格为2.4元，司机一个下午的营业额是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若 x 满足 (9x)(x4)=4， 求 (4x)2+(x9)2 的值.

    设 9x=a，x4=b， 则 (9x)(x4)=ab=4，a+b=(9x)+(x4)=5 ，

    ∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13

    请仿照上面的方法求解下面问题：

    (1)若 x 满足 (5x)(x2)=2， 求 (5x)2+(x2)2 的值

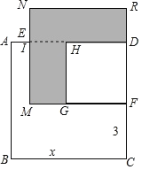
    (2)已知正方形 ABCD 的边长为 x ， E ， F 分别是 AD 、 DC 上的点，且 AE=1 ， CF=3 ，长方形 EMFD 的面积是 48 ，分别以 MF 、 DF 作正方形，求阴影部分的面积.

    查看答案和解析>>

    同步练习册答案