
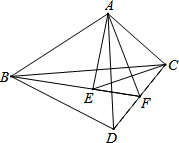
 如图,△ABC,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①BE=CD;②FA平分∠EFC;③FE=FD;④FE+FC=FA;其中一定正确的结论有( )个.
如图,△ABC,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①BE=CD;②FA平分∠EFC;③FE=FD;④FE+FC=FA;其中一定正确的结论有( )个.| A、1 | B、2 | C、3 | D、4 |
|
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2.015×109元 |
| B、2.015×107元 |
| C、2.015×1011元 |
| D、2.015×106元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
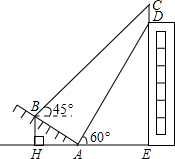 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com