
【题目】如图,已知一次函数的图象y=kx+b与反比例函数y=﹣ ![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求:
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,求: 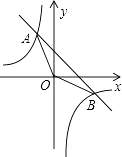
(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
【答案】
(1)解:令反比例函数y=﹣ ![]() 中x=﹣2,则y=4,
中x=﹣2,则y=4,
∴点A的坐标为(﹣2,4);
反比例函数y=﹣ ![]() 中y=﹣2,则﹣2=﹣
中y=﹣2,则﹣2=﹣ ![]() ,解得:x=4,
,解得:x=4,
∴点B的坐标为(4,﹣2).
∵一次函数过A、B两点,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为y=﹣x+2
(2)解:设直线AB与y轴交于C,
令为y=﹣x+2中x=0,则y=2,
∴点C的坐标为(0,2),
∴S△AOB= ![]() OC(xB﹣xA)=
OC(xB﹣xA)= ![]() ×2×[4﹣(﹣2)]=6
×2×[4﹣(﹣2)]=6
(3)解:观察函数图象发现:
当x<﹣2或0<x<4时,一次函数图象在反比例函数图象上方,
∴一次函数的函数值大于反比例函数的函数值时x的取值范围为x<﹣2或0<x<4
【解析】(1)由点A、B的横纵坐标结合反比例函数解析式即可得出点A、B的坐标,再由点A、B的坐标利用待定系数法即可得出直线AB的解析式;(2)设直线AB与y轴交于C,找出点C的坐标,利用三角形的面积公式结合A、B点的横坐标即可得出结论;(3)观察函数图象,根据图象的上下关系即可找出不等式的解集.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】综合与探究
阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
(1)数轴上有理数﹣10与﹣5对应的两点之间的距离等于 ;数轴上有理数x与﹣5对应的两点之间的距离用含x的式子表示为 ;若数轴上有理数x与﹣1对应的两点A,B之间的距离|AB|=2,则x等于 ;
联系拓广:
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择 题.
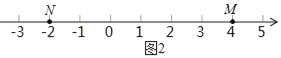
A.①若点P在点M,N两点之间,则|PM|+|PN|= ;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于 .
B.①若点P在点M,N之间,则|x+2|+|x﹣4|= ;
若|x+2|+|x﹣4|═10,则x= ;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小芳从家骑自行车去学校,所需时间y(min)与骑车速度x(m/min)之间的反比例函数关系如图.
(1)小芳家与学校之间的距离是多少?
(2)写出y与x的函数表达式;
(3)若小芳7点20分从家出发,预计到校时间不超过7点28分,请你用函数的性质说明小芳的骑车速度至少为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: 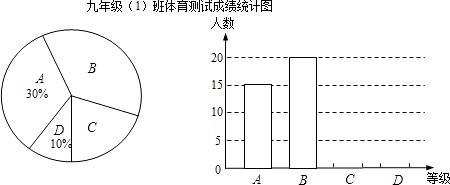
(1)九年级(1)班参加体育测试的学生有人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 , 等级C对应的圆心角的度数为;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数![]() ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,小芳到操场上测量旗杆的高度,她的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,利用她所测数据,求旗杆的高.
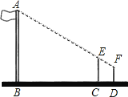
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从南京站开往上海站的一辆和谐号动车,中途只停靠苏州站,甲、乙、丙3名互不相识的旅客同时从南京站上车.
(1)求甲、乙、丙三名旅客在同一个站下车的概率;
(2)求甲、乙、丙三名旅客中至少有一人在苏州站下车的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com