
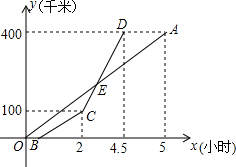
 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:分析 (1)设线段CD对应的函数解析式为y=kx+b,由待定系数法求出其解即可;
(2)根据两图象相交的交点指的是两车相遇解答即可.
(3)先由货车和轿车相距30千米列出方程解答即可.
解答 解:(1)设线段CD对应的函数解析式为y=kx+b,
可得:$\left\{\begin{array}{l}{100=2k+b}\\{400=4.5k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=120}\\{b=-140}\end{array}\right.$.
所以线段CD对应的函数表达式为:y=120x-140(2≤x≤4.5);
(2)由图象可得:直线OA的解析式为:y=80x,
根据两图象相交的交点指的是两车相遇,
可得:80x=120x-140,
解得:x=3.5,
把x=3.5代入y=80x,得:y=280;
所以E点的坐标为(3.5,280),即表示当货车出发3.5小时时货车和轿车相遇;
(3)设货车出发xh后,
可得:120x-140-30=80x,
解得:x=4.25.
故答案为:4.25.
由题意知,B($\frac{1}{3}$,0),
∴BC段解析式为y=60x-20($\frac{1}{3}$≤x≤2),
货车与轿车相距30km有四种情况:
1)当$\frac{1}{3}$≤x≤2时,80x-(60x-20)=30,解得x=$\frac{1}{2}$;
2)当2<x≤$\frac{7}{2}$时,80x-(120x-140)=30,解得x=$\frac{11}{4}$;
3)当$\frac{7}{2}$<x≤$\frac{9}{2}$时,120x-140-80x=30,解得x=$\frac{17}{4}$;
4)当$\frac{9}{2}$<x≤5时,400-80x=30,解得x=$\frac{37}{8}$;
∴x=$\frac{1}{2}、\frac{11}{4}、\frac{17}{4}、\frac{37}{8}$.
点评 本题考查了一次函数的应用,对一次函数图象的意义的理解,待定系数法求一次函数的解析式的运用,行程问题中路程=速度×时间的运用,本题有一定难度,其中求出货车与轿车的速度是解题的关键.


科目:初中数学 来源: 题型:选择题
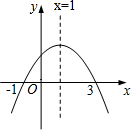 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2-4ac>0; ②2a+b<0;③9a+3b+c=0;④a:b:c=-1:2:3.其中正确的是( )| A. | ①② | B. | ②③ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-2,0)或(2,10).
如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(-2,0)或(2,10).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
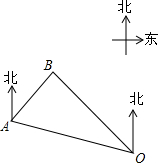 如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com