
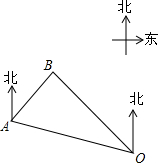
 如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449) 分析 作BC⊥OA于点C,根据题意得∠MAB=45°,∠NOA=60°,∠NOB=30°,OA=60海里.由AM∥ON,求出∠BAO=∠MAO-∠MAB=75°,根据三角形内角和定理得出∠ABO=180°-∠BAO-∠AOB=75°,利用等角对等边得到OB=OA=60海里,在直角△OBC中根据含30°角的直角三角形的性质得出BC=$\frac{1}{2}$OB=30海里,OC=$\sqrt{3}$BC=30$\sqrt{3}$海里,那么AC=OA-OC=(60-30$\sqrt{3}$)≈8.04海里,然后根据勾股定理求出AB=$\sqrt{A{C}^{2}+B{C}^{2}}$≈31.1海里.
解答 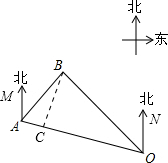 解:如图,作BC⊥OA于点C,根据题意得∠MAB=45°,∠NOA=60°,∠NOB=30°,OA=60海里.
解:如图,作BC⊥OA于点C,根据题意得∠MAB=45°,∠NOA=60°,∠NOB=30°,OA=60海里.
∵AM∥ON,
∴∠MAO+∠NOA=180°,
∴∠MAO=180°-∠NOA=120°,
∴∠BAO=∠MAO-∠MAB=75°,
∵∠AOB=∠NOA-∠NOB=30°,
∴∠ABO=180°-∠BAO-∠AOB=75°,
∴∠BAO=∠ABO=75°,
∴OB=OA=60海里,
∴BC=$\frac{1}{2}$OB=30海里,OC=$\sqrt{3}$BC=30$\sqrt{3}$海里,
∴AC=OA-OC=(60-30$\sqrt{3}$)≈8.04海里,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$≈$\sqrt{8.0{4}^{2}+3{0}^{2}}$≈31.1海里.
答:A、B两地之间的距离约为31.1海里.
点评 本题考查了解直角三角形的应用-方向角问题,平行线的性质,等腰三角形的判定,三角形内角和定理,含30°角的直角三角形的性质,勾股定理.求出∠BAO=∠ABO=75°是解题的关键.


科目:初中数学 来源: 题型:解答题
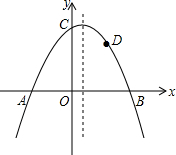 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
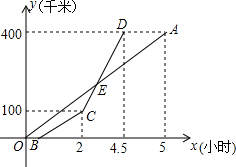 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
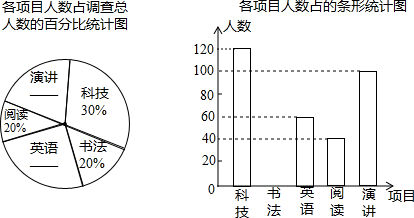
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-1<b-1 | B. | -3a>-2b | C. | a>b-16 | D. | $\frac{a}{5}<\frac{b}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批节能灯泡的使用寿命 | |
| B. | 了解某班同学“跳绳”的成绩 | |
| C. | 了解全国每天丢弃的塑料袋的数量 | |
| D. | 了解上海卫视“今晚80后”栏目的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com