
【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求![]() 的值.
的值.
【答案】1.
【解析】分析:利用等式的性质将(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2变形成(x﹣y)2+(x﹣z)2+(y﹣z)2=0的形式,从而得到x=y=z,再求得![]() 的值.
的值.
详解:
∵(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
∴(y﹣z)2﹣(y+z﹣2x)2+(x﹣y)2﹣(x+y﹣2z)2+(z﹣x)2﹣(z+x﹣2y)2=0,
∴(y﹣z+y+z﹣2x)(y﹣z﹣y﹣z+2x)+(x﹣y+x+y﹣2z)(x﹣y﹣x﹣y+2z)+(z﹣x+z+x﹣2y)(z﹣x﹣z﹣x+2y)=0,
∴2x2+2y2+2z2﹣2xy﹣2xz﹣2yz=0,
∴(x﹣y)2+(x﹣z)2+(y﹣z)2=0.
∵x,y,z均为实数,
∴x=y=z.
∴![]() =
=![]() =1.
=1.


科目:初中数学 来源: 题型:
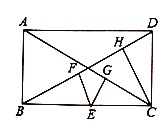
【题目】(1)如图,已知矩形![]() 中,点
中,点![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 三者之间具有怎样的数量关系,并证明你的猜想;
三者之间具有怎样的数量关系,并证明你的猜想;
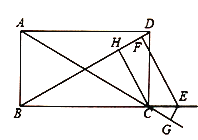
(2)如图,若点![]() 在矩形
在矩形![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() ,则线段
,则线段![]() 三者之间具有怎样的数量关系,直接写出你的结论;
三者之间具有怎样的数量关系,直接写出你的结论;
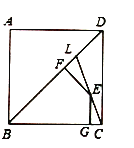
(3)如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上任一点,
上任一点,![]() 与点
与点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 之间具有怎样的数量关系,直接写出你的猜想.
之间具有怎样的数量关系,直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连接AC,EC.已知AB=5,DE=2,BD=12,设CD=x.
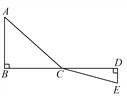
(1)用含x的代数式表示AC+CE的长;
(2)请问点C在BD上什么位置时,AC+CE的值最小?
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M(n,-n)在第二象限,过点M的直线y=kx+b(k>1)分别交x轴、y轴于点A、B,过点M作MN⊥x轴于点N,点P为线段AN上任意一点,则点P的横坐标可以是( )
A. (1+![]() )nB. (1+
)nB. (1+![]() )nC. (1+k)nD. (1-k)n
)nC. (1+k)nD. (1-k)n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 1×2=![]() (1×2×3-0×1×2),2×3=
(1×2×3-0×1×2),2×3=![]() (2×3×4-1×2×3),3×4=
(2×3×4-1×2×3),3×4=![]() (3×4×5- 2×3×4),
(3×4×5- 2×3×4),
由以上三个等式左、右两边分别相加,可得:
1×2+2×3+3×4=![]() ×3×4×5=20
×3×4×5=20
读完以上材料,请你计算下列各题(写出过程):
(1)1×2+2×3+3×4+…+10×11= ;
(2)1×2+2×3+3×4+…+n×(n+1)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司决定更换节能环保的新型公交车,购买的数量和所需费用如下表所示:
(1)求A型和B型公交车的单价:
(2)该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次;公交公司该如何购买这10辆公交车,才能确保公交车的年均载客量的总和不少于670万人次,且所需费用最省,并求出最省的费用

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com