
【题目】某公交公司决定更换节能环保的新型公交车,购买的数量和所需费用如下表所示:
(1)求A型和B型公交车的单价:
(2)该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次;公交公司该如何购买这10辆公交车,才能确保公交车的年均载客量的总和不少于670万人次,且所需费用最省,并求出最省的费用

【答案】(1)A:100万元,B:150万元;(2)当A型公交车8辆时,最低费用为680万元
【解析】
(1)根据“购买A型公交车3辆,B型公交车1辆,共需450万元;若购买A型公交车2辆,B型公交车3辆,共需650万元”列方程组求解可得;
(2)设购买A型公交车x辆,则购买B型公交车(10-x)辆,根据“这10辆公交车年均载客量总和不少于670万人次”求得x的范围即可.
解:(1)设A、B分别为x,y元/辆;
![]() ,解得x=100,y=150.
,解得x=100,y=150.
(2)设购买A型公交车x辆,则购买B型公交车(10-x)辆,
根据题意得:60x+100(10-x)≥670,
解得:x≤8![]() ,
,
∵x>0,且10-x>0,
∴0<x<8![]() ,
,
∴x最大整数为8,
所以当m=8时,最低费用为680万元.


科目:初中数学 来源: 题型:
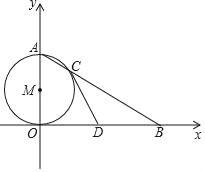
【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣![]() 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】字母m、n分别表示一个有理数,且m≠n.现规定min{m,n}表示m、n中较小的数,例如:min{3,﹣1}=﹣1,min{﹣1,0}=﹣1.据此解决下列问题:
(1)min{﹣![]() ,﹣
,﹣![]() }= .
}= .
(2)若min{![]() ,2)=﹣1,求x的值;
,2)=﹣1,求x的值;
(3)若min{2x﹣5,x+3}=﹣2,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B在数轴上表示的数如图所示. 动点P从点A出发,沿数轴向右以每秒2个单位长度的速度运动到点B,再从点B以同样的速度运动到点A停止,设点P运动的时间为t秒,解答下列问题.
![]()
(1)当t=2时,AP= 个单位长度,当t=6时,AP= 个单位长度;
(2)直接写出整个运动过程中AP的长度(用含t的代数式表示);
(3)当AP=6个单位长度时,求t的值;
(4)当点P运动到线段AB的3等分点时,t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
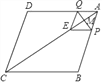
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②如果欲求![]() 的值,可令
的值,可令
![]() ……………①
……………①
将①式右边顺序倒置,得![]() ……………②
……………②
由②加上①式,得2![]() ;
;
∴ S=_________________;
由结论求![]() ;
;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②为了求![]() 的值,可令
的值,可令![]() ,则
,则![]() ,因此
,因此![]() ,所以
,所以![]() ,
,
即![]() .
.
仿照以上推理,计算![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com