
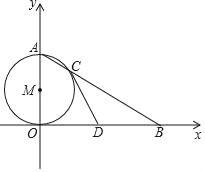
【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
【答案】(1)B(2![]() ,0);(2)见解析
,0);(2)见解析
【解析】分析:(1)由点A的坐标可知OA的长度,根据∠ABO的度数可知AB的长度为4,利用勾股定理即可求出OB的长度,从而求出B的坐标.
(2)连接OC、MC、证明∠OCB为直角,根据D为OB的中点,可知∠DCO=∠DOC,易知∠OCM=∠COM,所以∠MCO+∠DCO=∠MCD=90°,即可求证MC⊥CD.
详解:(1)∵A的坐标为(0,2)
∴OA=2,
∵∠ABO=30°,∠AOB=90°,
∴AB=2OA=4,
∴由勾股定理可知:OB=2![]() ,
,
∴B(2![]() ,0)
,0)
(2)连接OC,MC
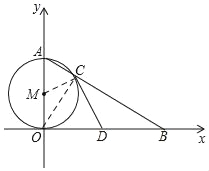
∵OA是⊙M的直径,
∴∠ACO=90°,
∴∠OCB=90°,
在Rt△OCB中,D为OB的中点,
∴CD=![]() OB=OD,
OB=OD,
∴∠DCO=∠DOC,
∵MC=MO,
∴∠OCM=∠COM
∵∠MOC+∠DOC=∠AOB=90°,
∴∠MCO+∠DCO=∠MCD=90°
即MC⊥CD
∴直线CD是⊙M的切线.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1.例:[0.5]=﹣0.5.
(1)求[![]() ]、[﹣1]的值;
]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b],试求代数式(b﹣a)3﹣3a+3b的值;
(3)解方程:[x]+[x+2]=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为体现社会对教师的尊重,今年教师节出租节司机小王在东西方向的公路上免费接送教师,如果规定向东为正,向西为负,出租车的行程如下(单位:km):
+15,-4,+13,-10,-12,+3,-13,-17
(1)最后一名教师被送到目的地时,小王在出发地的什么位置?
(2)若汽车耗油量为0.12L/km,小王出发前加满了40L油,当他送完最后一名教师后,问他能否开车顺利返回?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
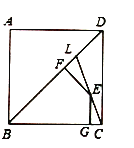
【题目】(1)如图,已知矩形![]() 中,点
中,点![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 三者之间具有怎样的数量关系,并证明你的猜想;
三者之间具有怎样的数量关系,并证明你的猜想;
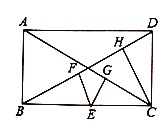
(2)如图,若点![]() 在矩形
在矩形![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() ,则线段
,则线段![]() 三者之间具有怎样的数量关系,直接写出你的结论;
三者之间具有怎样的数量关系,直接写出你的结论;
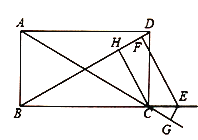
(3)如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上任一点,
上任一点,![]() 与点
与点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 之间具有怎样的数量关系,直接写出你的猜想.
之间具有怎样的数量关系,直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两名选手参加长跑比赛,乙从起点出发匀速跑到终点,甲先快后慢,半个小时后找到适合自己的速度,匀速跑到终点,他们所跑的路程y(单位:km)随时间x(单位:h)变化的图象,如图所示,则下列结论错误的是( )
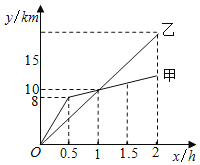
A. 在起跑后1h内,甲在乙的前面
B. 跑到1h时甲乙的路程都为10km
C. 甲在第1.5时的路程为11km
D. 乙在第2h时的路程为20km
查看答案和解析>>
科目:初中数学 来源: 题型:
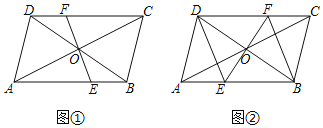
【题目】在ABCD中,对角线AC,BD相交于点O.EF过点O且与ABCD分别相交于点E,F
(1)如图①,求证:OE=OF;
(2)如图②,若EF⊥DB,垂足为O,求证:四边形BEDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
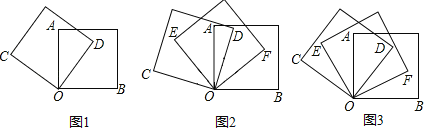
【题目】已知正方形的每个角等于90°,请解决下列问题:
(1)如图1,将两个正方形的一个顶点O重合放置,若∠AOD=50°,求∠COB的度数;
(2)如图2,将三个正方形的一个顶点O重合放置,若∠EOC=40°,∠BOF=30°,求∠AOD的度数;
(3)如图3,将三个正方形的一个顶点O重合放置,若OF平分∠DOB,那么OE平分∠AOC吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司决定更换节能环保的新型公交车,购买的数量和所需费用如下表所示:
(1)求A型和B型公交车的单价:
(2)该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次;公交公司该如何购买这10辆公交车,才能确保公交车的年均载客量的总和不少于670万人次,且所需费用最省,并求出最省的费用

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com