
分析 (1)首先提取公因式(x+2)得到(x+2)(x+2-2)=0,然后解两个一元一次方程即可;
(2)首先找出a=3,b=-8,c=-3,然后利用公式法求出一元二次方程的解即可.
解答 解:(1)∵(x+2)2=2x+4,
∴(x+2)2-2(x+2)=0,
∴(x+2)(x+2-2)=0,
∴x+2=0或x=0,
∴x1=-2,x2=0;
(2)∵3x2-8x-3=0,
∴a=3,b=-8,c=-3,
∴b2-4ac=(-8)2-4×3(-3)=100,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-(-8)±\sqrt{100}}{2×3}$=$\frac{8±10}{6}$,
∴x1=-$\frac{1}{3}$,x2=3.
点评 本题主要考查了因式分解法以及公式法解一元二次方程的知识,解答本题的关键是熟练掌握因式分解法和公式法解方程的步骤,此题难度一般.


科目:初中数学 来源: 题型:选择题
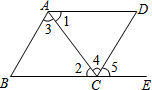 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )| A. | ①②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
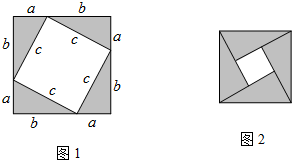 阅读下面的材料
阅读下面的材料查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com