
【题目】甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( )
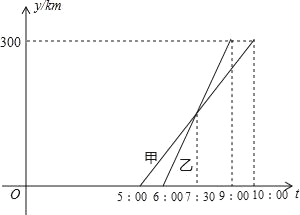
A. A城和B城相距300km
B. 甲先出发,乙先到达
C. 甲车的速度为60km/h,乙车的速度为100km/h
D. 6:00~7:30乙在甲前,7:30甲追上乙,7:30~9:00甲在乙前
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
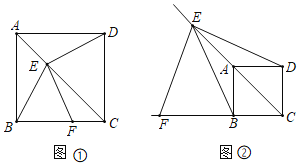
【题目】感知:如图①,在正方形![]() 中,点
中,点![]() 在对角线
在对角线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连结
重合),连结![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .易知
.易知![]() ,进而证出
,进而证出![]() .
.
探究:如图②,点![]() 在射线
在射线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连结
重合),连结![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
应用:如图②,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
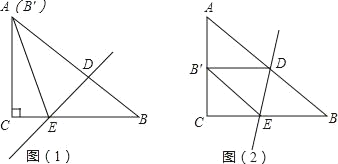
【题目】在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,顶点B的对应点是B′.
(1)如图(1),如果点B′和顶点A重合,求CE的长;
(2)如图(2),如果点B′和落在AC的中点上,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,E是AB延长线上一点,分别以AB、BE为一边在直线AE同侧作正方形ABCD和正方形BEFG,连接AG、CE.
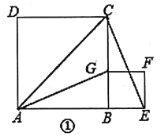
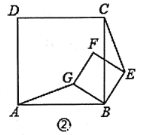
(1)试探究线段AG与CE的大小关系,并证明你的结论;
(2)若AG恰平分∠BAC,且BE=1,试求AB的长;
(3)将正方形BEFG绕点B逆时针旋转一个锐角后,如图②,问(1)中结论是否仍然成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图1所示的程序,得到了如图y与x的函数图像,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图像于点P、Q,连接OP、OQ.则以下结论:①x<0 时,y=![]() ;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM⑤∠POQ可以等于90°.其中正确结论序号是( )
;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM⑤∠POQ可以等于90°.其中正确结论序号是( )
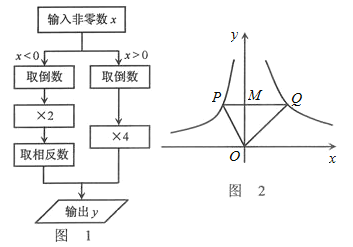
A.①②③B.②③④C.③④⑤D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥![]() 于点D.
于点D.
(1)如图①,当直线![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次暑假旅游中,小明在湖泊的游船上(A处),测得湖西岸的山峰(C处)和湖东岸的山峰(D处)的仰角都是45°,游船向东航行100米后到达B处,测得C、D两处的仰角分别为30°,60°,试求出C、D两座山的高度为多少米?(结果保留整数)(![]() ≈1.73)
≈1.73)
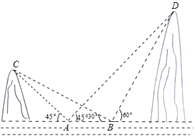
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果![]() ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=x2-4x-5与x轴分别交于A、B(A在B的左边),与y轴交于点C,直线AP与y轴正半轴交于点M,交抛物线于点P,直线AQ与y轴负半轴交于点N,交抛物线于点Q,且OM=ON,过P、Q作直线l
(1) 探究与猜想:
① 取点M(0,1),直接写出直线l的解析式
取点M(0,2),直接写出直线l的解析式
② 猜想:
我们猜想直线l的解析式y=kx+b中,k总为定值,定值k为__________,请取M的纵坐标为n,验证你的猜想
(2) 如图2,连接BP、BQ.若△ABP的面积等于△ABQ的面积的3倍,试求出直线l的解析式

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com