
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式
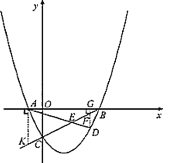
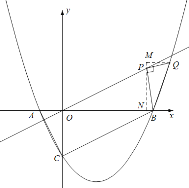
(2)如图1,点![]() 为第四象限抛物线上一点,连接
为第四象限抛物线上一点,连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
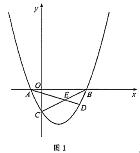
(3)如图2,连接![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,点
,点![]() ,
,![]() 分别为直线和抛物线上的点.试探究:在第一象限是否存在这样的点
分别为直线和抛物线上的点.试探究:在第一象限是否存在这样的点![]() ,
,![]() ,使
,使![]() .若存在,请求出所有符合条件的点
.若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或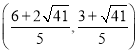
【解析】
(1)利用待定系数法进行求解即可;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() ,则可得△AEK∽△DEF,继而可得
,则可得△AEK∽△DEF,继而可得![]() ,先求出BC的解析式,继而求得AK长,由
,先求出BC的解析式,继而求得AK长,由![]() 可得
可得![]() ,设点
,设点![]() ,进而可得
,进而可得![]() ,从而可得
,从而可得![]() ,再利用二次函数的性质即可求得答案;
,再利用二次函数的性质即可求得答案;
(3)先确定出∠ACB=90°,再得出直线![]() 的表达式为
的表达式为![]() .设点
.设点![]() 的坐标为
的坐标为![]() ,然后分点
,然后分点![]() 在直线
在直线![]() 右侧,点
右侧,点![]() 在直线
在直线![]() 左侧两种情况分别进行讨论即可.
左侧两种情况分别进行讨论即可.
(1)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
∴ ,
,
∴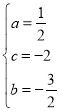 ,
,
∴抛物线的函数表达式为![]() ;
;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() .
.
则DG//AK,
∴△AEK∽△DEF,
∴![]() ,
,
设直线BC的解析式为y=kx+n,
将![]() 、
、![]() 代入则有:
代入则有:![]() ,
,
解得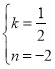 ,
,
∴直线![]() 的表达式为
的表达式为![]() ,
,
当x=-1时,![]() ,
,
即K(-1,![]() ),
),
∴![]() .
.
∵![]() .
.
∴![]()
设点![]() ,则F点坐标为(m,
,则F点坐标为(m,![]() ),
),
∴![]() .
.
∴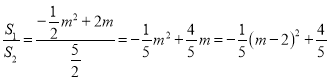 ,
,
当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
(3)∵![]() ,
,![]() ,
,![]() .
.
∴AC=![]() ,BC=
,BC=![]() ,AB=5,
,AB=5,
∴AC2+BC2=25=52=AB2,
∴∠ACB=90°,
∵过点![]() 作直线
作直线![]() ,直线
,直线![]() 的表达式为
的表达式为![]() ,
,
∴直线![]() 的表达式为
的表达式为![]() .
.
设点![]() 的坐标为
的坐标为![]() .
.
①当点![]() 在直线
在直线![]() 右侧时,如图,∠BPQ=90°,过点P作PN⊥x轴于点N,过点Q作QM⊥PN于点M,
右侧时,如图,∠BPQ=90°,过点P作PN⊥x轴于点N,过点Q作QM⊥PN于点M,
∴∠M=∠PNB=90°,
∴∠BPN+∠PBN=90°,
∵∠QPM+∠BPN=180°-∠QPB=180°-90°=90°,
∴∠QPM=∠PBN,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵NB=t-4,PN=![]() ,
,
∴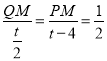 ,
,
∴QM=![]() ,PM=
,PM=![]() ,
,
∴MN=![]() +
+![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
将点![]() 的坐标为
的坐标为![]() 代入
代入![]() ,得
,得
![]() ,
,
解得:![]() ,t2=0(舍去),
,t2=0(舍去),
此时点![]() 的坐标为
的坐标为![]() .
.
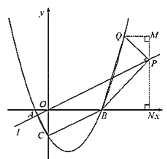
②当点![]() 在直线
在直线![]() 左侧时.如图,∠BPQ=90°,过点P作PN⊥x轴于点N,过点Q作QM⊥PN于点M,
左侧时.如图,∠BPQ=90°,过点P作PN⊥x轴于点N,过点Q作QM⊥PN于点M,
∴∠M=∠PNB=90°,
∴∠BPN+∠PBN=90°,
∵∠QPM+∠BPN=180°-∠QPB=180°-90°=90°,
∴∠QPM=∠PBN,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵NB=4-t,PN=![]() ,
,
∴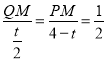 ,
,
∴QM=![]() ,PM=
,PM=![]() ,
,
∴MN=![]() +
+![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
将点![]() 的坐标为
的坐标为![]() 代入
代入![]() ,得
,得
![]() ,
,
解得:![]() ,
,![]() <0(舍去),
<0(舍去),
此时点![]() 的坐标为
的坐标为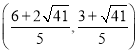 .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD.下列四个结论:①AC
的中点,连接CD、OD.下列四个结论:①AC![]() OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
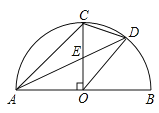
A.①④B.①②④C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
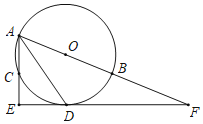
【题目】如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC得延长线于点E,延长线ED交AB得延长线于点F.
(1)判断直线EF与⊙O的位置关系,并证明.
(2)若DF=![]() ,求tan∠EAD的值.
,求tan∠EAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的边
的边![]() 上取一点
上取一点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画⊙O,⊙O与边
为半径画⊙O,⊙O与边![]() 相切于点
相切于点![]() ,
,![]() ,连接
,连接![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() ,并延长交线段
,并延长交线段![]() 于点
于点![]() .
.
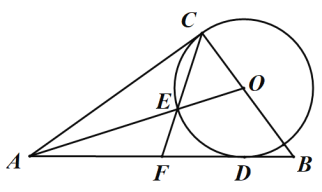
(1)求证:![]() 是⊙O的切线;
是⊙O的切线;
(2)若![]() ,
,![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若![]() 是
是![]() 的中点,试探究
的中点,试探究![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC中AB边上一点,以点O为圆心,OA的长为半径作⊙O,⊙O恰好经过点C,且与边BC,AB分别交于E,F两点.连接AE,过点E作⊙O的切线,交线段BF于点M,交AC的延长线于点N,且EM=BM,EB=AO.
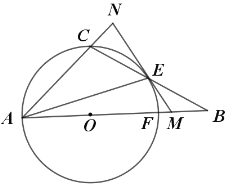
(1)求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).△AOB绕点O逆时针旋转90°后得到△A1OB1.
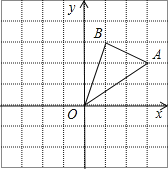
(1)点A关于点O中心对称的点的坐标为 ;
(2)点A1的坐标为 ;
(3)在旋转过程中,求线段AB扫过的面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com