
【题目】已知等腰梯形ABCD中,AB∥CD,对角线AC、BD相交于O,∠ABD=30°,AC⊥BC,AB=8cm,则△COD的面积为( )
A.![]()
cm2
B.![]()
cm2
C.![]()
cm2
D.![]()
cm2
【答案】A
【解析】解:∵梯形ABCD是等腰梯形,CD∥AB,
由SAS可证△DAB≌△CBA,
∴∠CAB=∠DCA=30°,
∵∠CAB=30°,又因为AC⊥BC,
∴∠DAB=∠CBA=60°,
∴∠DAC=∠DCA=30°,
∴CD=AD=BC=4cm,
∴AC2=AB2﹣BC2 ,
∴AC=4 ![]() cm,
cm,
∵梯形ABCD是等腰梯形,
∴AC=BD=4 ![]() cm,
cm,
∴S△ABC= ![]() ×4×4
×4×4 ![]() =8
=8 ![]() cm2 ,
cm2 ,
设DO为x,则CO=x,则AO=BO=(4 ![]() ﹣x)cm,
﹣x)cm,
在Rt△COB中,CO2+BC2=BO2 ,
即:x2+42=(4 ![]() ﹣x)2
﹣x)2
∴D0= ![]() cm,
cm,
∴S△ADO= ![]() ×
× ![]() ×4=
×4= ![]() ,
,
∴S△AOB=S△ABC﹣S△ADO= ![]()
∵AB∥CD,
∴△AOB∽△DOC,
∴( ![]() )2=
)2= ![]()
∴S△DOC= ![]() ,
,
故选:A.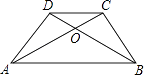
【考点精析】掌握等腰梯形的性质是解答本题的根本,需要知道等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.


科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
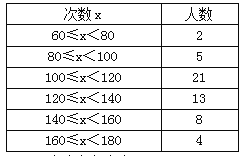
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,属于二元一次方程的个数有( )
①xy+2x-y=7; ②4x+1=x-y; ③![]() +y=5; ④x=y; ⑤x2-y2=2
+y=5; ④x=y; ⑤x2-y2=2
⑥6x-2y ⑦x+y+z=1 ⑧y(y-1)=2y2-y2+x
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五子棋深受广大棋友的喜爱,其规则是:在 15 15 的正方形棋盘中,由黑方先行,轮流奕子,在任何一方向(横向、竖向或斜线 方向)上连成五子者为胜。如图 3 是两个五子棋爱好者甲和乙的 部分对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若 A 点的位置记作(8,4),若不让乙在短时间内获胜,则甲必须落子 的位置是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查. 
通过随机抽样调查50家客户,得到如下数据:
A B B A B B A C A C A B A D A A B
B A A D B A B A C A C B A A D A A
A B B D A A A B A C A B D A B A
(1)请你补全下面的数据统计表: 家装风格统计表
装修风格 | 划记 | 户数 | 百分比 |
A中式 | 正正正正正 | 25 | 50% |
B欧式 | |||
C韩式 | 5 | 10% | |
D其他 | 正 | 10% | |
合计 | 50 | 100% |
(2)请用扇形统计图描述(1)表中的统计数据;(注:请标明各部分的圆心角度数)
(3)如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于![]() 的二元一次方程组
的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)若上述方程组的解是等腰三角形的腰和底边的长,且这个等腰三角形周长为9,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com