
【题目】已知,在![]() 中,
中,![]() 点
点![]() 为
为![]() 的中点.
的中点.
![]() 问题发现
问题发现
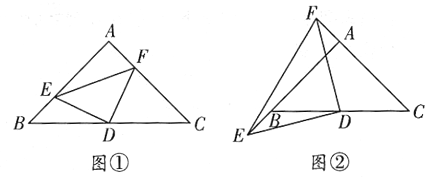
如图①,若点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 则线段
则线段![]() 与
与![]() 的数量关系是 ___ _,线段
的数量关系是 ___ _,线段![]() 与
与![]() 的位置关系是 ___ _;
的位置关系是 ___ _;
![]() 拓展探究
拓展探究
如图②,若点![]() 分别是
分别是![]() 上的点,且
上的点,且![]() 连接
连接![]() 上述结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
上述结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
![]() 解决问题
解决问题
当点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() 连接
连接![]() 直接写出
直接写出![]() 的面积.
的面积.
【答案】(1)![]() ;(2)结论成立,
;(2)结论成立,![]() ,证明见解析;(3)10
,证明见解析;(3)10
【解析】
(1)利用三角形中位线的性质,先证明四边形EFDB和四边形EFCD是平行四边形,再根据平行四边形的性质即可得到答案;
(2) 连接![]() ,证
,证![]() ,根据
,根据![]() 即可算出答案;
即可算出答案;
(3) 连接![]() ,求出
,求出![]() ,根据三角形的面积公式即可得到答案;
,根据三角形的面积公式即可得到答案;
解:![]() ,
,
证明:若点![]() 分别是
分别是![]() 的中点,
的中点,
则EF是三角形ABC的中位线,
又∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴四边形EFDB和四边形EFCD是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴∠EFD=∠B=45°,∠FED=∠C=45°(平行四边形对角相等),
∴![]() ,
,
∴∠EDF=180°-45°-45°=90°,
∴![]() ;
;
(2)结论成立,![]()
证明:如解图①,连接![]()
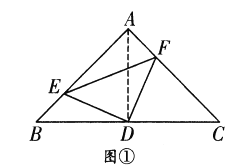
![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
![]() 且
且![]() 平分
平分![]()
![]()
在![]() 和
和![]() 中,
中,
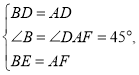
![]() ,
,
![]()
![]() ,
,
![]()
即![]()
即![]() ;
;
(3)三角形![]() 的面积为
的面积为![]() .
.
如解图②,连接![]()
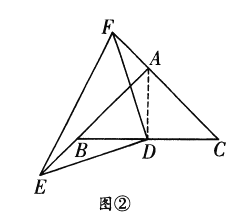
![]()
![]() 为等腰三角形,
为等腰三角形,
![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
![]()
![]()
![]()
又![]()
![]() ,
,
![]()
![]()
![]() 为等腰直角三角形.
为等腰直角三角形.
![]()
![]()
在![]() 中,
中,![]()
![]()
![]() ;
;


科目:初中数学 来源: 题型:
【题目】由于世界人口增长、水污染以及水资源浪费等原因,全世界面临着淡水资源不足的问题,我国是世界上严重缺水的国家之一.节约用水是水资源合理利用的关键所在,是最快捷、最有效、最可行的维护水资源可持续利用的途径之一,为了调查居民的用水情况,有关部门对某小区的20户居民的月用水量进行了调查,数据如下(单位![]() ):
):
6.7 8.7 7.3 11.4 7.0 6.9 11.7 9.7 10.0 9.7
7.3 8.4 10.6 8.7 7.2 8.7 10.5 9.3 8.4 8.7
整理数据:按如下分段整理样本数据并补充表格(表1):
用水量 |
|
|
|
|
人数 |
| 6 | b | 4 |
分析数据:补全下列表格中的统计量(表2):
平均数 | 中位数 | 众数 |
8.85 |
| 8.7 |
得出结论:
(1)表中的![]() ,
,![]() ,
,![]() ;
;
(2)若用表1中的数据制作一个扇形统计图,![]() 所占的扇形圆心角的度数为 度;
所占的扇形圆心角的度数为 度;
(3)如果该小区有住户400户,根据样本估计用水量在![]() 的居民有多少户?
的居民有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
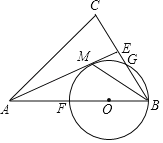
【题目】已知:如图,在△ABC中,AB=AC,AE是∠CAB的角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=6,cosC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
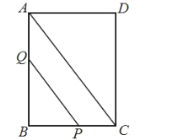
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点、过点
边上的一个动点、过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() ,把线段
,把线段![]() 绕点
绕点![]() 旋转至
旋转至![]() (点
(点![]() 与点
与点![]() 对应),点
对应),点![]() 落在线段
落在线段![]() 上,若
上,若![]() 恰好平分
恰好平分![]() ,则
,则![]() 的长为_________.
的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在等腰直角![]() 中,斜边
中,斜边![]() .
.

(1)请你在图①的![]() 边上求作一点
边上求作一点![]() ,使得
,使得![]() ;
;
(2)如图②,在(1)问的条件下,将![]() 边沿
边沿![]() 方向平移,使得点
方向平移,使得点![]() 、
、![]() 、
、![]() 对应点分别为
对应点分别为![]() 、
、![]() 、
、![]() ,连接
,连接![]() ,
,![]() .若平移的距离为1,求
.若平移的距离为1,求![]() 的大小及此时四边形
的大小及此时四边形![]() 的面积;
的面积;
(3)将![]() 边沿
边沿![]() 方向平移
方向平移![]() 个单位至
个单位至![]() ,是否存在这样的
,是否存在这样的![]() ,使得在直线
,使得在直线![]() 上有一点
上有一点![]() ,满足
,满足![]() ,且此时四边形
,且此时四边形![]() 的面积最大?若存在,求出四边形
的面积最大?若存在,求出四边形![]() 面积的最大值及平移距离
面积的最大值及平移距离![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,过点B作BD⊥AB,点C,D都在AB上方,AD交△BCD的外接圆⊙O于点E.
(1)求证:∠CAB=∠AEC.
(2)若BC=3.
①EC∥BD,求AE的长.
②若△BDC为直角三角形,求所有满足条件的BD的长.
(3)若BC=EC=![]()
![]() ,则
,则![]() = .(直接写出结果即可)
= .(直接写出结果即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西贺州市)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1:y=![]() x2+c,当其函数值y=1时,只有一个自变量x的值与其对应
x2+c,当其函数值y=1时,只有一个自变量x的值与其对应
(1)求c的值;
(2)将抛物线l1经过平移得到抛物线l2:y=![]() (x﹣p)2﹣1.
(x﹣p)2﹣1.
①若抛物线l2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,记△ABC的外心为P,当﹣1≤p≤![]() 时,求点P的纵坐标的取值范围;
时,求点P的纵坐标的取值范围;
②当0≤x≤2时,对于抛物线l1上任意点E,抛物线l2上总存在点F,使得点E、F纵坐标相等,求p的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com