
【题目】已知:如图①,在等腰直角![]() 中,斜边
中,斜边![]() .
.

(1)请你在图①的![]() 边上求作一点
边上求作一点![]() ,使得
,使得![]() ;
;
(2)如图②,在(1)问的条件下,将![]() 边沿
边沿![]() 方向平移,使得点
方向平移,使得点![]() 、
、![]() 、
、![]() 对应点分别为
对应点分别为![]() 、
、![]() 、
、![]() ,连接
,连接![]() ,
,![]() .若平移的距离为1,求
.若平移的距离为1,求![]() 的大小及此时四边形
的大小及此时四边形![]() 的面积;
的面积;
(3)将![]() 边沿
边沿![]() 方向平移
方向平移![]() 个单位至
个单位至![]() ,是否存在这样的
,是否存在这样的![]() ,使得在直线
,使得在直线![]() 上有一点
上有一点![]() ,满足
,满足![]() ,且此时四边形
,且此时四边形![]() 的面积最大?若存在,求出四边形
的面积最大?若存在,求出四边形![]() 面积的最大值及平移距离
面积的最大值及平移距离![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)详见解析;(2)![]() ,
,![]() ;(3)存在,当
;(3)存在,当![]() 时,四边形
时,四边形![]() 面积最大值为
面积最大值为![]()
【解析】
(1)利用等腰三角形“三线合一”的性质,取AC中点为点P即可.
(2)延长AP、CD相交于点M,取AB的中点F,连接PF.证明△APE≌△MPD,得到AP=MP,从而可得PF是△ABM的中位线.进而得到PF是AB的垂直平分线,这样可以得出∠APB=2∠M=2∠EAP.由AE=PE可得∠M=∠MPD=∠EPA=∠EAP,所以可得∠PDB=2∠M,由AC∥ED可得∠PDB=∠ACB=45°,所以∠APB=45°.
(3)如图,以AB为边长,在直线AB的右侧作等边三角形ABO,在以O为圆心、OA长为半径作⊙O.过点O作OM⊥AC,交⊙O于点M,点M在AC的右上方.过点M作AC的平行线DE,AE∥BC,BC的延长线交DE于点D.则此时满足∠AMB=30°,此时四边形ABDE的面积最大.
解:(1)利用等腰三角形的“三线合一”性质,取AC的中点P,连接BP即可,如下图所示:
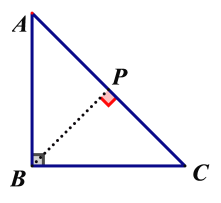
(2)如下图所示:
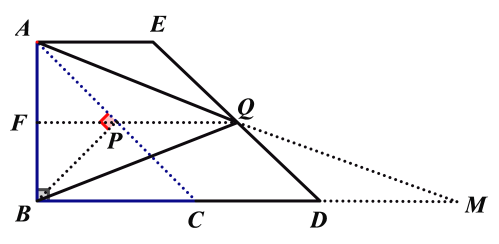
延长AQ、CD相交于点M,取AB的中点F,连接PF.
由平移的性质可得,DE=AC=2,AE=CD=1,AC∥DE,AE∥CD
设∠EAQ=x
∵点Q是DE的中点∴QE=QD=![]() DE=1
DE=1
∴QE=AE
∴∠AQE=∠EAQ=x,∴∠MQD=∠AQE=x
∵AE∥CD ∴∠M=∠EAQ=x
在△AQE和△MQD中
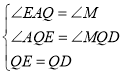 ,∴△AQE≌△MQD(AAS)
,∴△AQE≌△MQD(AAS)
∴AQ=MQ
∵点F是AB的中点
∴QF是△ABM的中位线
∵由题知,∠ABC=90°
∴∠AFQ=90°
∴PF⊥AB,点F是AB的中点
∴BQ=AQ=MQ
∴∠QBM=∠M=x
∴∠AQB=∠QBM+∠M=2x
由题知∠ACB=45°且AC∥DE
∴∠QDB=∠ACB=45°
∵∠QDB=∠MQD+∠M=2x
∴2x=45°即∠AQB=45°
在等腰直角△ABC中,斜边AC=2,则AB=BC=![]()
∴BD=BC+CD=![]()
∴四边形ABDE的面积为:![]()
故答案为:![]() ,
,![]() .
.
(3) 存在.
如下图,以AB为边长,在直线AB的右侧作等边三角形ABO,在以O为圆心、OA长为半径作⊙O.过点O作OM⊥MD,交⊙O于点M,点M在AC的右上方.
过点M作AC的平行线DE,AE∥BC,BC的延长线交DE于点D,AE交⊙O于点H.
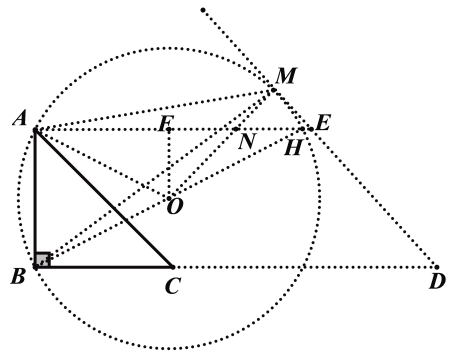
则此时满足∠AMB=30°,此时四边形ABDE的面积最大.
作OF⊥AE于F,OM与AE相交于点N.
∵AE∥CD,DE∥AC
∴四边形ACDE是平行四边形
∴AE=CD,DE=AC=2
∴∠EDC=∠ACB=45°
∴∠AEM=∠EDC=45°
∵OM⊥AC
∴OM⊥DE
∴∠NME=90°
∴NE=![]() MN,∠MNH=45°
MN,∠MNH=45°
由(2)知,AB=BC=![]()
∴⊙O的半径是![]() .
.
连接BH,∵AE∥BC,∠ABC=90°
∴∠BAH=180°-∠ABC=90°
∵∠AMB=30°,![]()
![]()
∴∠AHB=∠AMB=30°
∴![]()
∵OF⊥AH,点O是圆心
∴![]()
根据勾股定理得![]()
∵∠FNO=∠MNH=45°
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
![]()
故答案为:当![]() 时,四边形
时,四边形![]() 面积最大值为
面积最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,OA=3,OC=2,且BE∥AC,AE∥OB.
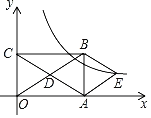
(1)求证:四边形AEBD是菱形;
(2)求经过点E的双曲线对应的函数解析式;
(3)设经过点E的双曲线与直线BE的另一交点为F,过点F作x轴的平行线,交经过点B的双曲线于点G,交y轴于点H,求△OFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
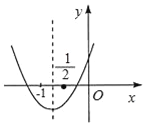
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时直线
;同时直线![]() 由点
由点![]() 出发沿
出发沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,运动过程中始终保持
,运动过程中始终保持![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() .
.
(1)![]() ___________,
___________,![]() __________,
__________,![]() _____________;(用含
_____________;(用含![]() 的式子表示)
的式子表示)
(2)当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值;
的值;
(3)当点![]() 在线段
在线段![]() 的垂直平分线上时,求
的垂直平分线上时,求![]() 的值;
的值;
(4)是否存在时刻![]() ,使以
,使以![]() 为直径的圆与
为直径的圆与![]() 的边相切?若存在,直接写出
的边相切?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
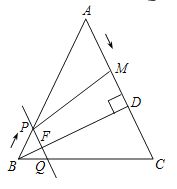
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一辆单车放在水平的地面上,车把头下方![]() 处与坐垫下方
处与坐垫下方![]() 处在平行于地面的同一水平线上,
处在平行于地面的同一水平线上,![]() ,
,![]() 之间的距离约为
之间的距离约为![]() ,现测得
,现测得![]() ,
,![]() 与
与![]() 的夹角分别为
的夹角分别为![]() 与
与![]() ,若点
,若点![]() 到地面的距离
到地面的距离![]() 为
为![]() ,坐垫中轴
,坐垫中轴![]() 处与点
处与点![]() 的距离
的距离![]() 为
为![]() ,求点
,求点![]() 到地面的距离(结果保留一位小数).(参考数据:
到地面的距离(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() )
)
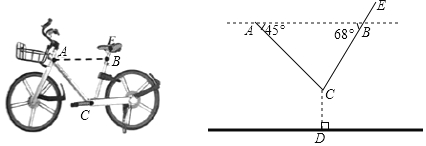
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() 点
点![]() 为
为![]() 的中点.
的中点.
![]() 问题发现
问题发现
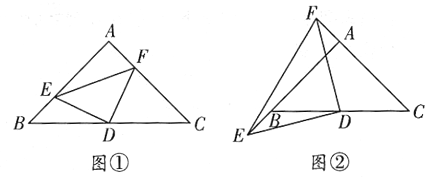
如图①,若点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 则线段
则线段![]() 与
与![]() 的数量关系是 ___ _,线段
的数量关系是 ___ _,线段![]() 与
与![]() 的位置关系是 ___ _;
的位置关系是 ___ _;
![]() 拓展探究
拓展探究
如图②,若点![]() 分别是
分别是![]() 上的点,且
上的点,且![]() 连接
连接![]() 上述结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
上述结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
![]() 解决问题
解决问题
当点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() 连接
连接![]() 直接写出
直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校学生每周参加课外辅导班的情况,随机调査了部分学生一周内参加课外辅导班的学科数,并将调查结果绘制成如图1、图2所示的两幅不完整统计图(其中A:0个学科,B:1个学科,C:2个学科,D:3个学科,E:4个学科或以上),请根据统计图中的信息,解答下列问题:
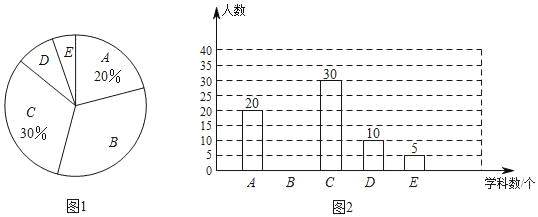
(1)请将图2的统计图补充完整;
(2)根据本次调查的数据,每周参加课外辅导班的学科数的众数是 个学科;
(3)若该校共有2000名学生,根据以上调查结果估计该校全体学生一周内参加课外辅导班在3个学科(含3个学科)以上的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
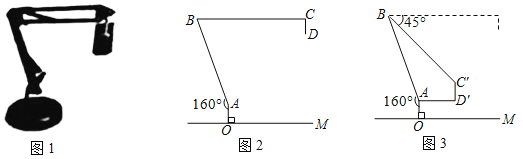
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
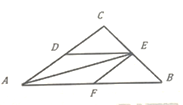
【题目】如图,在△ABC中,AB=3+![]() ,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com