
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,OA=3,OC=2,且BE∥AC,AE∥OB.
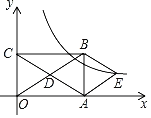
(1)求证:四边形AEBD是菱形;
(2)求经过点E的双曲线对应的函数解析式;
(3)设经过点E的双曲线与直线BE的另一交点为F,过点F作x轴的平行线,交经过点B的双曲线于点G,交y轴于点H,求△OFG的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先证明四边形AEBD是平行四边形,再证明DA=DB,即可得出结论;
(2)求出点E的坐标,即可求解;
(3)根据△OFG的面积S=S△OHG﹣S△OHF,即可求解.
解:(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形.
∵四边形OABC是矩形,
∴DA=![]() AC,DB=
AC,DB=![]() OB,AC=OB.
OB,AC=OB.
∴DA=DB.
∴平行四边形AEBD是菱形.
(2)如图1,连接DE,交AB于点M,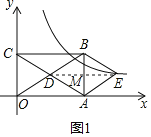
∵四边形AEBD是菱形,
∴AB与DE互相垂直且平分.
∵OA=3,OC=2,
∴EM=DM=![]() OA=
OA=![]() ,AM=
,AM=![]() AB=1.
AB=1.
∴点E的坐标为(![]() ,1).
,1).
设经过点E的反比例函数解析式为y=![]() ,
,
把点E(![]() ,1)代得k=
,1)代得k=![]() ,
,
∴双曲线的函数解析式为y=![]() .
.
(3)设经过点B的反比例函数解析式为y=![]() ,
,
把点B(3,2)代入得k1=6,
∴经过点B的反比例函数解析式为y=![]() .
.
∵直线FG∥x轴(如图2),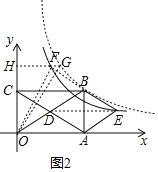
△OFG的面积S=S△OHG-S△OHF=![]() |k1|-
|k1|-![]() |k|=
|k|=![]() ×6-
×6-![]() ×
×![]() .
.


科目:初中数学 来源: 题型:
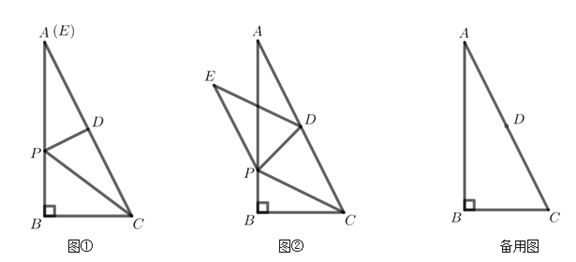
【题目】在Rt△ABC中,∠B=90°,BC=4,AB=8,点D是边AC的中点,动点P在边AB上(点P不与点A重合),连接PD、PC,将△PDC沿直线PD翻折,点C落在点E处得△PDE.
(1)如图①,若点E恰好与点A重合,求线段AP的长;
(2)如图②,若ED交AB于点F,四边形CDEP为菱形,求证:△PFE≌△AFD;
(3)连接AE,设△PDE与△ABC重叠部分的面积为S1,△PAC的面积为S2,若S1=![]() S2时,请直接写出tan∠AED的值.
S2时,请直接写出tan∠AED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
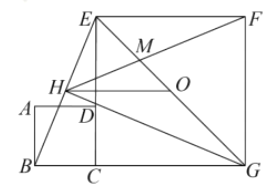
【题目】如图,正方形![]() 和正方形
和正方形![]() 的顶点
的顶点![]() 在同一条直线上,顶点
在同一条直线上,顶点![]() 在同一条直线上.
在同一条直线上.![]() 是
是![]() 的中点,
的中点,![]() 的平分线
的平分线![]() 过点
过点![]() ,交
,交![]() 于点
于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() 连接
连接![]() .以下四个结论:①
.以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
![]() ,其中正确的结论是____.
,其中正确的结论是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
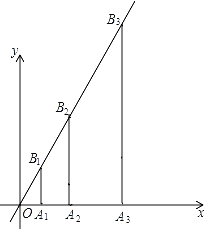
【题目】如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点B10的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于世界人口增长、水污染以及水资源浪费等原因,全世界面临着淡水资源不足的问题,我国是世界上严重缺水的国家之一.节约用水是水资源合理利用的关键所在,是最快捷、最有效、最可行的维护水资源可持续利用的途径之一,为了调查居民的用水情况,有关部门对某小区的20户居民的月用水量进行了调查,数据如下(单位![]() ):
):
6.7 8.7 7.3 11.4 7.0 6.9 11.7 9.7 10.0 9.7
7.3 8.4 10.6 8.7 7.2 8.7 10.5 9.3 8.4 8.7
整理数据:按如下分段整理样本数据并补充表格(表1):
用水量 |
|
|
|
|
人数 |
| 6 | b | 4 |
分析数据:补全下列表格中的统计量(表2):
平均数 | 中位数 | 众数 |
8.85 |
| 8.7 |
得出结论:
(1)表中的![]() ,
,![]() ,
,![]() ;
;
(2)若用表1中的数据制作一个扇形统计图,![]() 所占的扇形圆心角的度数为 度;
所占的扇形圆心角的度数为 度;
(3)如果该小区有住户400户,根据样本估计用水量在![]() 的居民有多少户?
的居民有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
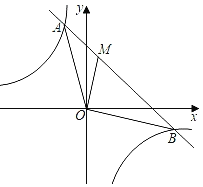
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于点A(﹣1,4)和点B(4,n).
的图象相交于点A(﹣1,4)和点B(4,n).
(1)求这两个函数的解析式;
(2)已知点M在线段AB上,连接OA,OB,OM,若S△AOM=![]() S△BOM,求点M的坐标.
S△BOM,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在等腰直角![]() 中,斜边
中,斜边![]() .
.

(1)请你在图①的![]() 边上求作一点
边上求作一点![]() ,使得
,使得![]() ;
;
(2)如图②,在(1)问的条件下,将![]() 边沿
边沿![]() 方向平移,使得点
方向平移,使得点![]() 、
、![]() 、
、![]() 对应点分别为
对应点分别为![]() 、
、![]() 、
、![]() ,连接
,连接![]() ,
,![]() .若平移的距离为1,求
.若平移的距离为1,求![]() 的大小及此时四边形
的大小及此时四边形![]() 的面积;
的面积;
(3)将![]() 边沿
边沿![]() 方向平移
方向平移![]() 个单位至
个单位至![]() ,是否存在这样的
,是否存在这样的![]() ,使得在直线
,使得在直线![]() 上有一点
上有一点![]() ,满足
,满足![]() ,且此时四边形
,且此时四边形![]() 的面积最大?若存在,求出四边形
的面积最大?若存在,求出四边形![]() 面积的最大值及平移距离
面积的最大值及平移距离![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com