
【题目】如图,正方形![]() 和正方形
和正方形![]() 的顶点
的顶点![]() 在同一条直线上,顶点
在同一条直线上,顶点![]() 在同一条直线上.
在同一条直线上.![]() 是
是![]() 的中点,
的中点,![]() 的平分线
的平分线![]() 过点
过点![]() ,交
,交![]() 于点
于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() 连接
连接![]() .以下四个结论:①
.以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
![]() ,其中正确的结论是____.
,其中正确的结论是____.
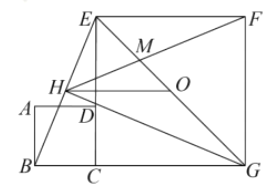
【答案】①②③
【解析】
①先利用正方形的性质证明![]() ,然后有
,然后有![]() ,通过等量代换可得
,通过等量代换可得![]() ,则
,则![]() ,即可判断①的正误;
,即可判断①的正误;
②通过直角三角形斜边中线的性质得出点H在正方形CGFE的外接圆上,然后根据圆周角定理的推论得出![]() ,即可判断②的正误;
,即可判断②的正误;
③首先证明![]() ,则有
,则有![]() ,进而可得
,进而可得![]() ,由此可判断③的正误;
,由此可判断③的正误;
④先得出![]() 是
是![]() 的中位线,则
的中位线,则![]() ,然后根据平行线分线段成比例得出
,然后根据平行线分线段成比例得出 ![]() ,则有
,则有![]() ,进而可求出
,进而可求出![]() ,又因为
,又因为![]() ,则可判断④的正误.
,则可判断④的正误.
∵四边形ABCD和四边形CGFE是正方形,
∴![]() .
.
在![]() 和
和![]() 中,
中,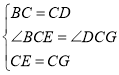
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,故①正确;
,故①正确;
![]() 是直角三角形,
是直角三角形,![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() 点H在正方形CGFE的外接圆上.
点H在正方形CGFE的外接圆上.
![]() ,
,
![]() ,
,
![]() ,故②正确;
,故②正确;
∵GH平分![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,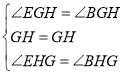
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,故③正确;
,故③正确;
∵四边形CGFE是正方形,
∴![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 与
与![]() 高相同,
高相同,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,故④错误.
,故④错误.
故答案为:①②③.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
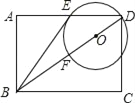
【题目】已知:如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD,BD分别交于点E、点F,且∠ABE=∠DBC.
(1)判断直线BE与⊙O的位置关系,并证明你的结论;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小昕的口袋中有5把相似的钥匙,其中2把钥匙(记为A1,A2)能打开教室前门锁,而剩余的3把钥匙(记为B1,B2,B3)不能打开教室前门锁.
(1)小昕从口袋中随便摸出一把钥匙就能打开教室前门锁的概率是 ;
(2)请用树状图或列表等方法,求出小昕从口袋中第一次随机摸出的一把钥匙不能打开教室前门锁(摸出的钥匙不再放回),而第二次随机摸出的一把钥匙正好能打开教室前门锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是( )
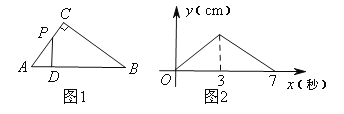
A.1.5cmB.1.2cmC.1.8cmD.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A. 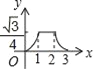 B.
B.  C.
C. 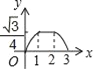 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,OA=3,OC=2,且BE∥AC,AE∥OB.
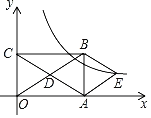
(1)求证:四边形AEBD是菱形;
(2)求经过点E的双曲线对应的函数解析式;
(3)设经过点E的双曲线与直线BE的另一交点为F,过点F作x轴的平行线,交经过点B的双曲线于点G,交y轴于点H,求△OFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时直线
;同时直线![]() 由点
由点![]() 出发沿
出发沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,运动过程中始终保持
,运动过程中始终保持![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() .
.
(1)![]() ___________,
___________,![]() __________,
__________,![]() _____________;(用含
_____________;(用含![]() 的式子表示)
的式子表示)
(2)当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值;
的值;
(3)当点![]() 在线段
在线段![]() 的垂直平分线上时,求
的垂直平分线上时,求![]() 的值;
的值;
(4)是否存在时刻![]() ,使以
,使以![]() 为直径的圆与
为直径的圆与![]() 的边相切?若存在,直接写出
的边相切?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com