
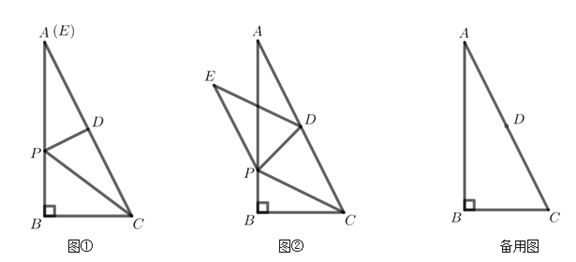
����Ŀ����Rt��ABC�У���B=90�㣬BC=4��AB=8����D�DZ�AC���е㣬����P�ڱ�AB��(��P�����A�غ�)������PD��PC������PDC��ֱ��PD���ۣ���C���ڵ�E���á�PDE��
��1����ͼ�٣�����Eǡ�����A�غϣ����߶�AP�ij���
��2����ͼ�ڣ���ED��AB�ڵ�F���ı���CDEPΪ���Σ���֤����PFE�ա�AFD��
��3������AE�����PDE���ABC�ص����ֵ����ΪS1����PAC�����ΪS2����S1=![]() S2ʱ����ֱ��д��tan��AED��ֵ��
S2ʱ����ֱ��д��tan��AED��ֵ��
���𰸡���1��AP=5����2��֤������������3��3��![]() ��
��
��������
��1�����ݷ��۵����ʵ�AP=PC����AP=x�����ݹ��ɶ����г����̣����x��ֵ���ɣ�
��2���������ε����ʵó�PE��CD��PE=CD���ڸ��ݴ�������D��AC���е�ɵó�AD=PE��PE��AC��Ȼ���Ƴ���PFE�ա�AFD��
��3������S1=![]() S2�Ƴ�AF=PF��EF=DF��Ȼ������������������ͼ���ٹ�D��DM��AP�ڵ�M����C��CN��PD�ڵ�N���ڹ�D��DM��AP�ڵ�M���ٷֱ���㼴�ɣ�
S2�Ƴ�AF=PF��EF=DF��Ȼ������������������ͼ���ٹ�D��DM��AP�ڵ�M����C��CN��PD�ڵ�N���ڹ�D��DM��AP�ڵ�M���ٷֱ���㼴�ɣ�
��1���ߡ�PDE�ɡ�PDC��������
��AP=PC��
��AP=x��
�ߡ�B=90�㣬
����Rt��PBC��PC2=PB2+BC2��
��x2=��8-x��2+42��
���x=5��
��AP=5��
��2�����ı���CDPEΪ���Σ�
��PE��CD��PE=CD��
��D��AC���е㣬
��AD=CD��
��AD=PE��
��PE��CD��
��PE��AC��
���APE=��PAD����DEP=��ADE��
�ڡ�PFE���AFD��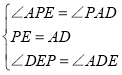 ��
��
���PFE�ա�AFD��
��3����D��AC�����꣬
��S��ADP=S��CDP=![]() S��PAC��
S��PAC��
���۵��ɵã�S��PDE=S��CDP��
��S��PDF=![]() S��PAC=
S��PAC=![]() S��ADP=
S��ADP=![]() S��PDE��
S��PDE��
��AF=PF��EF=DF��
����ͼ���ı���AEPD��ƽ���ı��Σ�
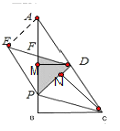
��D��DM��AP�ڵ�M����C��CN��PD�ڵ�N��
���AED=��EDP=��PDC��
�ߣ���B=90�㣬BC=4��AB=8��
��AC=![]() ��
��
��PC=PE=AD=![]() ��
��
��PB=![]() ��
��
��BM=![]() AB=4��DM=
AB=4��DM=![]() BC=2����λ�ߣ���
BC=2����λ�ߣ���
��PM=BM-PB=2��
��DP=![]() ��
��
��DN=![]() ��CN=
��CN=![]() ��
��
��tan��AED=tan��PDC=![]() =3��
=3��
����ͼ����D��DM��AP�ڵ�M
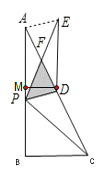 ��
��
��AP=DE=DC=![]() ��
��
��PM=![]() -4��
-4��
��tan��AED=tan��DPM=![]() ��
��
���ϣ�tan��AED��ֵΪ3��![]() ��
��


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() �У���
����![]() ��
��![]() ��������
��������![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��
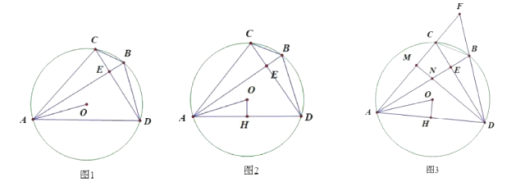
��1����֤��![]()
��2����ͼ2������![]() ��
��![]() ��������
������Ϊ��![]() ����֤��
����֤��![]()
��3����ͼ3���ڣ�2���������£��ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������l��y��x2+bx+c��x�ύ�ڵ�A�͵�B��3��0������y�ύ�ڵ�C��0����3����
��1����������l�Ķ���P������Ϊ��A�����ꣻ
��2����������l������ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ��õ�������l1����ֱ��д��ƽ�ƺ��������l1�ı���ʽ��
��3����������l����ƽ��m����λ���ȣ��õ�������l2�����е�A�Ķ�Ӧ��Ϊ��M������M��A��P��ǡ��һ�����ε��������㣬�����m��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
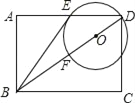
����Ŀ����֪����ͼ���ھ���ABCD�У���O�ڶԽ���BD�ϣ���OD�ij�Ϊ�뾶�ġ�O��AD��BD�ֱ��ڵ�E����F���ҡ�ABE=��DBC��
��1���ж�ֱ��BE���O��λ�ù�ϵ����֤����Ľ��ۣ�
��2����sin��ABE=![]() ��CD=2�����O�İ뾶��
��CD=2�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4���ֱ������1��2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���ȴӿڴ����������һ��С�������Ϊx��Сӱ��ʣ�µ�3�������������һ��С�������Ϊy������ȷ���˵�P(x��y)�����á��б���������״ͼ�������P(x��y)�ں���y=-x+5ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ż������ĸ��ٷ�չ�����ǵ�֧����ʽ�����˾�ı䣬ijѧϰС����������˴����ڼ�ij�̳��˿͵�֧����ʽ����Ҫ���ֽ�֧����������֧�����ֻ�֧���������֪ʹ��������֧����������Ϊ![]() ���ֻ�֧���ѳ�Ϊ��������֧����ʽ���ֻ�֧����Ҫ���������ַ�ʽ��
���ֻ�֧���ѳ�Ϊ��������֧����ʽ���ֻ�֧����Ҫ���������ַ�ʽ��![]() ~֧������
~֧������![]() ~�ţ�
~�ţ�![]() ~�������ֽ�ʹ���ֻ�֧����ʽ�����ĵ��������Ƴ����²�������ͳ��ͼ��
~�������ֽ�ʹ���ֻ�֧����ʽ�����ĵ��������Ƴ����²�������ͳ��ͼ��

��1������ͳ��ͼ�У�![]() ________���벹ȫ����ͳ��ͼ��
________���벹ȫ����ͳ��ͼ��
��2�������̳������ڼ乲20000�˹���������֧��������֧����������
��3��������ij��˿��ֽ�֧����������֧�����ֻ�֧��ÿ�ʽ�������ƽ�����ֱ�Ϊ120Ԫ��260Ԫ��80Ԫ��������˿�ÿ�ʽ���ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��ף�2020����ҹ��������¹ڷ������飬Ϊ������ѧ��������ͷ���Ԥ��֪ʶ���˽⣬ijѧУ�������翪չ�����֪ʶ�������������Ϊ�˽���ε�����Ч����ѧУ��ȫУ3600��ѧ���������ȡ200��ѧ������֪ʶ����(����100�֣��÷־�Ϊ����)����������200�˵IJ��Գɼ����ƶ�����ͳ��ͼ����

(1) ![]() ��
��![]() ���ɼ���õĵȼ�A��ռ�İٷֱȣ�
���ɼ���õĵȼ�A��ռ�İٷֱȣ�
(2)��������β����гɼ�Ϊ85�֣�����Ϊ85��һ������200��ѧ��֪ʶ���Գɼ�����λ����?���Ҫ˵�����ɣ�
(3)���80������(����80��)Ϊ���㣬�����ȫУ3600��ѧ���гɼ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С꿵Ŀڴ�����5�����Ƶ�Կ�ף�����2��Կ�ף���ΪA1��A2���ܴ���ǰ��������ʣ���3��Կ�ף���ΪB1��B2��B3�����ܴ���ǰ������
��1��С꿴ӿڴ����������һ��Կ���ܴ���ǰ�����ĸ������� ����
��2��������״ͼ���б��ȷ��������С꿴ӿڴ��е�һ�����������һ��Կ�ײ��ܴ���ǰ������������Կ�ײ��ٷŻأ������ڶ������������һ��Կ�������ܴ���ǰ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ĶԽ���OB��AC�ཻ�ڵ�D��OA��3��OC��2����BE��AC��AE��OB��
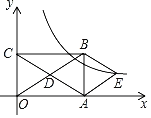
��1����֤���ı���AEBD�����Σ�
��2������E��˫���߶�Ӧ�ĺ�������ʽ��
��3���辭����E��˫������ֱ��BE����һ����ΪF������F��x���ƽ���ߣ���������B��˫�����ڵ�G����y���ڵ�H�����OFG�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com