
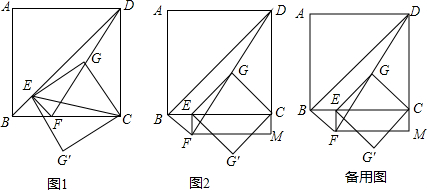
分析 (1)由直角三角形斜边上的中线等于斜边的一半可得出CG=$\frac{1}{2}$DF、EG=$\frac{1}{2}$DF,从而得出CG=EG,根据图形翻转的性质可知四边形EGCG′四条边相等,由此证出结论;
(2)连接BG、GM,由FE⊥BC于点E,且BE=EF可知△BEF为等腰直角三角形,结合∠DBC=45°即可得出∠DBF=90°,从而得出BG=$\frac{1}{2}$DF,同理亦可得出MG=$\frac{1}{2}$DF,即BG=MG,由FE⊥BC、FM⊥CD得出四边形EFMC为矩形,即BE=EF=MC,再由角与角间的关系可得出∠GBE=∠GMC,满足三角形的判定定义SAS,证出△GBE≌△GMC,即得出GE=GC结合(1)即可得出四边形EGCG′还是菱形;
(3)过点G′作G′N⊥CE于点N,由△GBE≌△GMC可得出∠BEG=∠MCG,由外角的性质及角与角间的关系可得出∠EGC=∠ECM=90°,结合等腰直角三角形的性质即可用x表示出G′N,由三角形的面积公式即可得出S关于x的函数关系式.
解答 证明:(1)∵四边形ABCD为正方形,
∴∠DCF=90°.
∵G为线段DF的中点,
∴CG=$\frac{1}{2}$DF.
∵FE⊥BD,
∴∠FED=90°,
∵G为线段DF的中点,
∴EG=$\frac{1}{2}$DF,
∴CG=EG.
∵将△EGC沿直线EC翻折到△EG′C,
∴CG=CG′,EG=EG′,
∴四边形EGCG′四条边相等,
∴四边形EGCG′是菱形.
(2)(1)中的结论”四边形EGCG′是菱形”依然成立.
证明:在图2中,连接BG,GM,如图所示.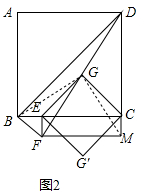
∵FE⊥BC于点E,且BE=EF,
∴△BEF为等腰直角三角形,
∴∠EBF=45°.
∵四边形ABCD为正方形,
∴∠DBE=45°,
∴∠DBF=∠DBE+∠EBF=90°.
∵G为线段DF的中点,
∴BG=$\frac{1}{2}$DF.
∵FM⊥CD于点M,
∴∠DMF=90°,
∵G为线段DF的中点,
∴MG=$\frac{1}{2}$DF,
∴BG=MG.
∵FE⊥BC,FM⊥CD,
∴四边形EFMC为矩形,
∴EF=CM.
∴BE=EF=MC.
∵BG=GD,MG=GD,
∴∠DBG=∠BDG,∠GMD=∠GDM,
∵∠DBC=∠CDB=45°,
∴∠GBE=∠DBC-∠DBG=45°-∠BDG,∠GMC=∠GDM=∠CBD-∠BDG=45°-∠BDG,
∴∠GBE=∠GMC.
在△GBE和△GMC中,有$\left\{\begin{array}{l}{BG=MG}\\{∠GBE=∠GMC}\\{BE=MC}\end{array}\right.$,
∴△GBE≌△GMC(SAS).
∴GE=GC.
∵将△EGC沿直线EC翻折到△EG′C,
∴CG=CG′,EG=EG′,
∴四边形EGCG′四条边相等,
∴四边形EGCG′是菱形.
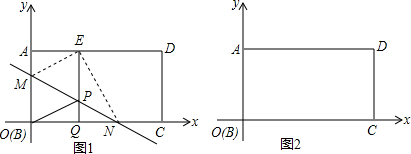
(3)在图2的基础上过点G′作G′N⊥CE于点N,如图3所示.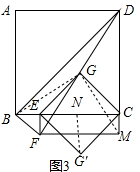
∵△GBE≌△GMC,
∴∠BEG=∠MCG,
∵∠BEG=∠EGC+∠ECG,∠MCG=∠MCG+∠ECM,
∴∠EGC=∠ECM=90°.
∴∠EG′C=90°,△EG′C为等腰直角三角形.
∵AB=4,BE=x,
∴EC=BC-BE=4-x,G′N=$\frac{1}{2}$EC=2-$\frac{x}{2}$.
四边形EGCG′的面积S=2×$\frac{1}{2}$EC•G′N=(4-x)(2-$\frac{x}{2}$)=$\frac{1}{2}$x2-4x+8(0<x<4).
点评 本题考查了直角三角形中线的性质、菱形的判定定理、三角形的面积公式、全等三角形的判定及性质、图形的翻转变换以及等腰直角三角形的性质,解题的关键:(1)找出CG=EG;(2)证明△GBE≌△GMC;(3)用含x的代数式表示G′N.本题属于中档题,(1)(3)难度不大;(2)难度不小,再证明GBE≌△GMC时,寻找∠GBE=∠GMC是难点.解决该题型题目时,通过全等三角形的性质寻找边角关系是关键.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
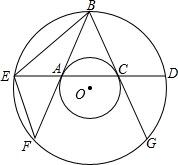 两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.
两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
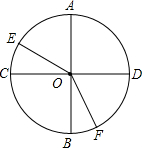 圆O的两条直径AB⊥CD,∠AOE=50°,∠DOF是∠BOF的2倍.
圆O的两条直径AB⊥CD,∠AOE=50°,∠DOF是∠BOF的2倍.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4226.3 | B. | 42.263 | C. | 0.042263 | D. | 42263000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
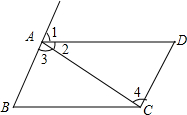 如图,由下列条件可以判定图中哪两条直线平行,说明理由
如图,由下列条件可以判定图中哪两条直线平行,说明理由查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com