
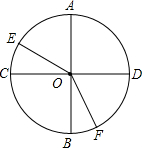
 圆O的两条直径AB⊥CD,∠AOE=50°,∠DOF是∠BOF的2倍.
圆O的两条直径AB⊥CD,∠AOE=50°,∠DOF是∠BOF的2倍.分析 (1)由AB⊥CD,∠AOE=50°,可求得∠COE=40°,由∠BOD=90,∠DOF是∠BOF的2倍,可求得∠BOF=30°即可求得结论;
(2)由于扇形COF的面积与扇形COE的面积比等于∠COF与∠COE之比,求出∠COF,∠COE即可.
解答 解:(1)∵AB⊥CD,∠AOE=50°,
∴∠COE=40°,∵∠BOD=90,∠DOF是∠BOF的2倍,
∴∠BOF=30°,
∴∠EOF=∠COE+∠BOF+∠BOC=160°;
(2)扇形COF的面积与扇形COE的面积比等于∠COF与∠COE之比,
∵∠COF=∠BOF+∠BOC=120,∠COE=40,
∴扇形COF的面积与扇形COE的面积比为120:40=3:1.
点评 本题主要考查了垂直定义,圆心角的定义,扇形的面积公式,熟练掌握扇形的计算公式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
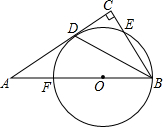 已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.
已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
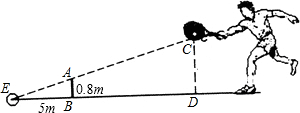 如图,小明打网球时能击中球的最高高度CD是2.4m,如果发球时要使球恰好能打过网AB,且落在离网5m的位置上,那么小明在离网多远的位置发球?
如图,小明打网球时能击中球的最高高度CD是2.4m,如果发球时要使球恰好能打过网AB,且落在离网5m的位置上,那么小明在离网多远的位置发球?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=$\sqrt{S}$ | B. | a=$\sqrt{S}$ | C. | S=$\sqrt{a}$ | D. | S=±$\sqrt{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
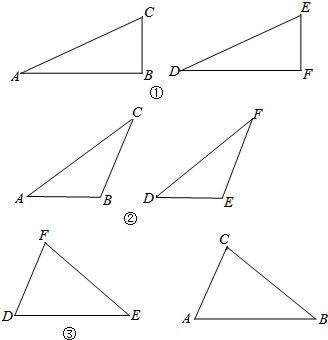
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com