
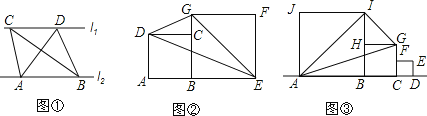
����Ŀ��̽������ͼ�٣�ֱ��l1��l2����A��B��ֱ��l1�ϣ���C��D��ֱ��l2�ϣ�����ABC�����ΪS1����ABD�����ΪS2����֤��S1��S2��
��չ����ͼ�ڣ�EΪ�߶�AB�ӳ�����һ�㣬BE��AB��������ABCD��������BEFG����ֱ��ABͬ�࣬��֤����DEG�������������BEFG�����һ�룮
Ӧ�ã���ͼ�ۣ���һ��ֱ���������е�A��B��C��D��������ABIJ��������BCGH��������CDEF����ֱ��ABͬ�࣬�ҵ�F��H�ֱ��DZ�CG��BI���е㣬��������CDEF�����Ϊl������AGI�����Ϊ�� ����
���𰸡�̽��������������չ����������Ӧ�ã�8![]()
��������
̽��������ƽ���ߵ����ʵõ���������������ͬ�ȸߵ����������Σ��������ǵ������ȣ�
��չ������BD�����������ε����ʿ�֪��GE��BD����DEG����BGEͬ�ȸߣ���S��DEG��S��BEG��������DEG�������������BEFG�����һ�룻
Ӧ�ã���������չ������˼·���н��
̽����֤������CM��l1�ڵ�M��DN��l1�ڵ�N����ͼ�٣�
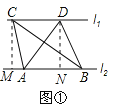
��l1��l2��
��CM��DN��
�֡ߡ�ABC����ABDͬ�ף�
��S1��S2��
��չ��֤��������BD����ͼ�ڣ�

���ı���ABCD���ı���BEFG��Ϊ�����Σ�
���ABD����BEG��45����
��BD��EG��
��̽���еĽ��ۿɵã�S��DEG��S��BEG��
��S��BEG��![]() S������BEFG��
S������BEFG��
��S��DEG��![]() S������BEFG��
S������BEFG��
Ӧ�ã��⣺������չ���ɵ�S��AGI��![]() S������ABIJ��
S������ABIJ��
��ͼ�ۣ�

��������CDEF�����Ϊl��
��CF��![]() ��
��
�ߵ�F��H�ֱ��DZ�CG��BI���е㣬
��BI��4![]() ����������ABIJ�ı߳�Ϊ4
����������ABIJ�ı߳�Ϊ4![]() ��
��
��S������ABIJ��16![]() ��
��
��S��AGI��8![]() ��
��
�ʴ��ǣ�8![]() ��
��


 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ������ԡ���У�ij����֧���Ըð�ȫ����Ա��һ�����������������������������ͳ�ƣ����Ƴ�����ͼ��ʾ��������������ͳ��ͼ��
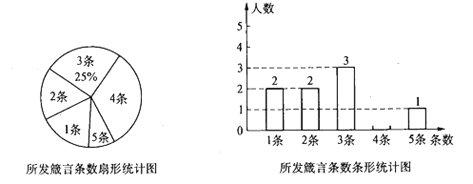
��1����ð���Ա����һ�������������Ե�ƽ�������Ƕ��٣�����������ͳ��ͼ����������
��2���������3�����Ե�ͬѧ������λ��ͬѧ������4�����Ե�ͬѧ������λŮͬѧ.��Ҫ�ӷ���3�����Ժ�4�����Ե�ͬѧ�зֱ�ѡ��һλ�μӸ�У��ί��֯�ġ����ԡ���ܽ�ᣬ�������б�������״ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
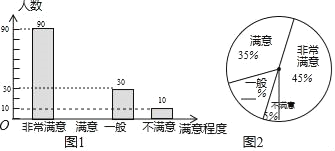
����Ŀ��Ϊ�˽������ȫ�д��Ĺ���������̶ȣ�¦����ij��ѧ��ѧ��ȤС����¦�׳�����Χ�ڽ����˳������飬����������Ϊ�dz����⣬���⣬һ�㣬���������࣬���ա�������ȫ���ʾ�������������������ͳ��ͼ1��ͼ2�����ͼ����Ϣ���ش�
��1���˴ι������˶���������
��2��������ͳ��ͼ�в������IJ��ֲ���������
��3�������г�������480000�˿ڣ���������жԴ��Ĺ������dz���������⡱������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2+��2m��1��x��2m��m��0.5������͵��������Ϊ��4��

��1���������ߵĽ���ʽ��
��2����ͼ1����������x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��DΪ�������ϵ�һ�㣬BDƽ���ı���ABCD����������D�����ꣻ
��3����ͼ2��ƽ��������y��x2+��2m��1��x��2m��ʹ�䶥��Ϊ����ԭ�㣬ֱ��y����2����һ����P������P������ֱ�ߣ��ֱ�����������Ψһ�Ĺ�����E��F��ֱ��PE��PF����y��ƽ�У�����֤��ֱ��EF���ijһ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��x2+bx�ĶԳ���Ϊx��1��������x��һԪ���η���x2+bx��t��0��Ϊʵ�����ک�1��x��4�ķ�Χ���н⣬��t��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
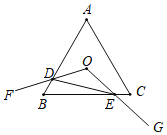
����Ŀ����ͼ���ȱ���ABC�ı߳�Ϊ4����O����ABC�����ģ���FOG��120�����Ƶ�O��ת��FOG���ֱ��߶�AB��BC��D��E���㣮����DE���������ĸ����ۣ���OD��OE����S��ODE��S��BDE����S�ı���ODBE��![]() ������BDE�ܳ�����СֵΪ6��������������ȷ�ĸ����ǣ� ��
������BDE�ܳ�����СֵΪ6��������������ȷ�ĸ����ǣ� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
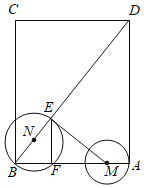
����Ŀ����ͼ���ھ���ABCD�У�AB��3��BC��4���뾶Ϊ1�Ķ�ԲԲ��M��A�����������AB������1����λ����/ÿ����ٶ������˶���ͬʱ����N�ӵ�B����������BD����Ҳ��1����λ����/ÿ����ٶ������˶������˶���ʱ��Ϊt�루0��t��2.5�����Ե�NΪԲ�ģ�NB�ij�Ϊ�뾶�ġ�N��BD��AB�Ľ���ֱ�ΪE��F������EF��ME��
��1���ٵ�t���� ����ʱ����Nǡ�þ�����M�������˶������У�����M����ABD�ı�����ʱ��t���� ���룻
��2������M������Bʱ������N��AD�ľ��룻�����N��AD�صõ��ҳ���
��3������N���߶�MEֻ��һ��������ʱ��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
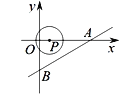
����Ŀ����ͼ��ֱ��![]() ��x���ڵ�A����y���ڵ�B����P��x����һ���㣬�Ե�PΪԲ�ģ���1����λ����Ϊ�뾶����P������P��ֱ��AB����ʱ����P�ĺ�������_____
��x���ڵ�A����y���ڵ�B����P��x����һ���㣬�Ե�PΪԲ�ģ���1����λ����Ϊ�뾶����P������P��ֱ��AB����ʱ����P�ĺ�������_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ǡ�O���һ�㣬CB���O�����ڵ�B��AC����O�ڵ�D����E��![]() �ϵ�һ�㣨�����A��B��D�غϣ�������C��48�������AED�Ķ���Ϊ_____��
�ϵ�һ�㣨�����A��B��D�غϣ�������C��48�������AED�Ķ���Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com