
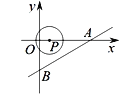
【题目】如图,直线![]() 交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的横坐标是_____
交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的横坐标是_____
【答案】![]()
【解析】
根据函数解析式求得A(3![]() ,0),B(0,-3),得到OA=3
,0),B(0,-3),得到OA=3![]() ,OB=3根据勾股定理得到AB=6,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=2,根据相似三角形的性质即可得到结论.
,OB=3根据勾股定理得到AB=6,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=2,根据相似三角形的性质即可得到结论.
∵直线![]() 交x轴于点A,交y轴于点B,
交x轴于点A,交y轴于点B,
∴令x=0,得y=-3,令y=0,得x=3![]() ,
,
∴A(3![]() ,0),B(0.-3),
,0),B(0.-3),
∴OA=3![]() ,OB=3,
,OB=3,
∴AB=6,
设⊙P与直线AB相切于D,连接PD,
则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴![]() ,
,
∴![]() ,
,
∴AP=2,
∴OP=3![]() -2或OP=3
-2或OP=3![]() +2,
+2,
∴P(3![]() -2,0)或P(3
-2,0)或P(3![]() +2,0),
+2,0),
故答案为:![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到六年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到六年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
类别 | 频数(人数) | 频率 |
武术类 | 0.25 | |
书画类 | 20 | 0.20 |
棋牌类 | 15 | b |
器乐类 | ||
合计 | a | 1.00 |
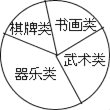
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.
请你根据以上图表提供的信息解答下列问题:
①a=_____,b=_____;
②在扇形统计图中,器乐类所对应扇形的圆心角的度数是_____;
③若该校六年级有学生560人,请你估计大约有多少学生参加武术类校本课程.
查看答案和解析>>
科目:初中数学 来源: 题型:
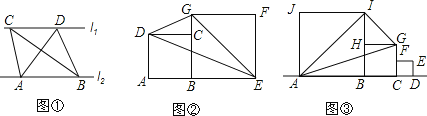
【题目】探究:如图①,直线l1∥l2,点A、B在直线l1上,点C、D在直线l2上,记△ABC的面积为S1,△ABD的面积为S2,求证:S1=S2.
拓展:如图②,E为线段AB延长线上一点,BE>AB,正方形ABCD、正方形BEFG均在直线AB同侧,求证:△DEG的面积是正方形BEFG面积的一半.
应用:如图③,在一条直线上依次有点A、B、C、D,正方形ABIJ、正方形BCGH、正方形CDEF均在直线AB同侧,且点F、H分别是边CG、BI的中点,若正方形CDEF的面积为l,则△AGI的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
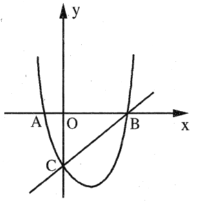
【题目】如图,二次函数的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() 是直线
是直线![]() 下方抛物线上一动点.
下方抛物线上一动点.
(1)求这个二次函数的表达式;
(2)连接![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 面积最大,若存在,求出点
面积最大,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)在平面直角坐标系中,对于函数图象的横宽、纵高给出如下定义:当自变量x在![]() 范围内时,函数值y满足
范围内时,函数值y满足![]() .那么我们称b-a为这段函数图象的横宽,称d-c为这段函数图象的纵高.纵高与横宽的比值记为k即:
.那么我们称b-a为这段函数图象的横宽,称d-c为这段函数图象的纵高.纵高与横宽的比值记为k即:![]() .
.
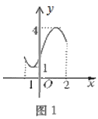
(示例)如图1,当![]() 时;函数值y满足
时;函数值y满足![]() ,那么该段函数图象的横宽为2-(-1)=3,纵高为4-1=3.则
,那么该段函数图象的横宽为2-(-1)=3,纵高为4-1=3.则![]() .
.
(应用)(1)当![]() 时,函数
时,函数![]() 的图象横宽为 ,纵高为 ;
的图象横宽为 ,纵高为 ;
(2)已知反比例函数![]() ,当点M(3,4)和点N在该函数图象上,且MN段函数图象的纵高为2时,求k的值.
,当点M(3,4)和点N在该函数图象上,且MN段函数图象的纵高为2时,求k的值.
(3)已知二次函数![]() 的图象与x轴交于A点,B点.
的图象与x轴交于A点,B点.
①若m=1,是否存在这样的抛物线段,当![]() (
(![]() )时,函数值满足
)时,函数值满足![]() 若存在,请求出这段函数图象的k值;若不存在,请说明理由.
若存在,请求出这段函数图象的k值;若不存在,请说明理由.
②如图2,若点P在直线y=x上运动,以点P为圆心,![]() 为半径作圆,当AB段函数图象的k=1时,抛物线顶点恰好落在
为半径作圆,当AB段函数图象的k=1时,抛物线顶点恰好落在![]() 上,请直接写出此时点P的坐标.
上,请直接写出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E,连接OC.
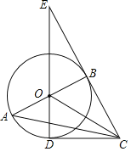
(1) 判断直线CD与⊙O的位置关系,并说明理由;
(2) 若BE=![]() ,DE=3,求⊙O的半径及AC的长.
,DE=3,求⊙O的半径及AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
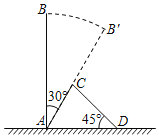
【题目】如图,某次台风来袭时,垂直于地面的大树AB被刮倾斜30°后,折断倒在地上,树的顶部恰好落在地面上点D处,大树被折断部分和地面所成的角∠ADC=45°,AD=4米,求这棵大树AB原来的高度是多少米?(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BC=kAC,点D在AC上,连接BD.
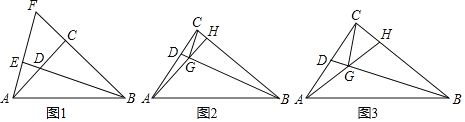
(1)如图1,当k=1时,BD的延长线垂直于AE,垂足为E,延长BC、AE交于点F.求证:CD=CF;
(2)过点C作CG⊥BD,垂足为G,连接AG并延长交BC于点H.
①如图2,若CH=![]() CD,探究线段AG与GH的数量关系(用含k的代数式表示),并证明;
CD,探究线段AG与GH的数量关系(用含k的代数式表示),并证明;
②如图3,若点D是AC的中点,直接写出cos∠CGH的值(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,AC=4,BC=3,点M、N分别是边AC、AB上的动点,连接MN,将△AMN沿MN所在直线翻折,翻折后点A的对应点为A′.
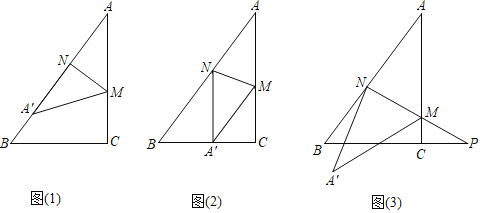
(1)如图1,若点A′恰好落在边AB上,且AN=![]() AC,求AM的长;
AC,求AM的长;
(2)如图2,若点A′恰好落在边BC上,且A′N∥AC.
①试判断四边形AMA′N的形状并说明理由;
②求AM、MN的长;
(3)如图3,设线段NM、BC的延长线交于点P,当![]() 且
且![]() 时,求CP的长.
时,求CP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com