
����Ŀ����ͼ����֪��ABC�У���ACB��90�㣬AC��4��BC��3����M��N�ֱ��DZ�AC��AB�ϵĶ��㣬����MN������AMN��MN����ֱ�߷��ۣ����ۺ��A�Ķ�Ӧ��ΪA�䣮
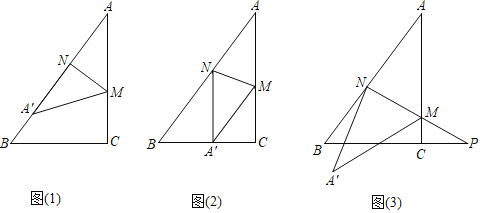
��1����ͼ1������A��ǡ�����ڱ�AB�ϣ���AN��![]() AC����AM�ij���
AC����AM�ij���
��2����ͼ2������A��ǡ�����ڱ�BC�ϣ���A��N��AC��
�����ж��ı���AMA��N����״��˵�����ɣ�
����AM��MN�ij���
��3����ͼ3�����߶�NM��BC���ӳ��߽��ڵ�P����![]() ��
��![]() ʱ����CP�ij���
ʱ����CP�ij���
���𰸡���1��![]() ����2�������Σ����ɼ���������AM=
����2�������Σ����ɼ���������AM=![]() ��MN��
��MN��![]() ����3��1��
����3��1��
��������
��1���������������ε�������⼴�ɣ�
��2���������ڱ���ȵ�ƽ���ı���������֤�����ɣ�
������AA�佻MN��O����AM��MA�䣽x����MA���AB���ɵ�![]() ��
��![]() ���ɴ˹����������x����ֱ�����������OM���ɽ�����⣮
���ɴ˹����������x����ֱ�����������OM���ɽ�����⣮
��3����ͼ3�У���NH��BC��H����취���NH��CM���������������Σ�ȷ��������ϵ���������̽�����⼴�ɣ�
�⣺��1����ͼ1�У�
��Rt��ABC�У��ߡ�C��90�㣬AC��4��BC��3��
��AB��![]() ��
��
�ߡ�A����A����ANM����C��90�㣬
���ANM�ס�ACB��
��![]() ��
��![]() ��
��
��AN��![]() AC
AC
��![]() ��
��![]() ��
��
��AM��![]() ��
��
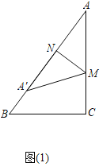
��2������ͼ2�У�
��NA���AC��
���AMN����MNA�䣬
�ɷ��ۿ�֪��MA��MA�䣬��AMN����NMA�䣬
���MNA�䣽��A��MN��
��A��N��A��M��
��AM��A��N����AM��A��N��
���ı���AMA��N��ƽ���ı��Σ�
��MA��MA�䣬
���ı���AMA��N�����Σ�
������AA�佻MN��O����AM��MA�䣽x��
��MA���AB��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
���x��![]() ��
��
��AM��![]()
��CM��![]() ��
��
��CA�䣽![]() ��
��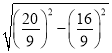 ��
��![]() ��
��
��AA�䣽![]() ��
�� ��
��![]() ��
��
���ı���AMA��N�����Σ�
��AA���MN��OM��ON��OA��OA�䣽![]() ��
��
��OM��![]() ��
�� ��
��![]() ��
��
��MN��2OM��![]() ��
��

��3����ͼ3�У���NH��BC��H��
��NH��AC��
���ABC�ס�NBH
��![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��![]()
��NH��![]() ��BH��
��BH��![]() ��
��
��CH��BC��BH��3��![]() ��
��![]() ��
��
��AM��![]() AC��
AC��![]() ��
��
��CM��AC��AM��4��![]() ��
��![]() ��
��
��CM��NH��
���CPM�ס�HPN
��![]() ��
��![]() ��
��
��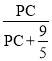 ��
��![]() ��
��
��PC��1��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
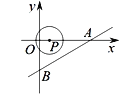
����Ŀ����ͼ��ֱ��![]() ��x���ڵ�A����y���ڵ�B����P��x����һ���㣬�Ե�PΪԲ�ģ���1����λ����Ϊ�뾶����P������P��ֱ��AB����ʱ����P�ĺ�������_____
��x���ڵ�A����y���ڵ�B����P��x����һ���㣬�Ե�PΪԲ�ģ���1����λ����Ϊ�뾶����P������P��ֱ��AB����ʱ����P�ĺ�������_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ǡ�O���һ�㣬CB���O�����ڵ�B��AC����O�ڵ�D����E��![]() �ϵ�һ�㣨�����A��B��D�غϣ�������C��48�������AED�Ķ���Ϊ_____��
�ϵ�һ�㣨�����A��B��D�غϣ�������C��48�������AED�Ķ���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�������������
2����4��8����16��32����64����
4����2��10����14��34����62����
��1��2����4��8����16��32����
�������������ĵ�n���У��������µ��������ֱ��Ϊa��b��c���۲���Щ�����ص㣬���������õ��Ĺ��ɣ��������Ϊ���⣮
��1���ú�n��ʽ�ӷֱ��ʾ��a��b��c��
��2�����ݣ�1���Ľ��ۣ���a��b��c�������ĺ�Ϊ770����n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
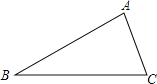
����Ŀ���߹���ͼ����֪��ABC����ͼ��
��1����������ABC�����Բ��O��
��2����AC��4����B��30�㣬���ABC�����Բ��O�İ뾶Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
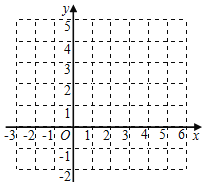
����Ŀ����֪���κ���y��x2��4x+3��
��1����������ƽ��ֱ������ϵ�л�������ͼ��
��2��������A��x1��y1����B��x2��y2����C��x3��y3����2��x1��x2��x3����y1��y2��y3�Ĵ�С��ϵΪ�� ����
��3����������ͼ�����ƽ�ƣ����Եõ�����y��x2��ͼ����д��һ��ƽ�Ʒ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨����ƽ��ֱ������ϵ�У������P������Ϊ��m��n��������![]() �����õ�P�������ʾΪ��
�����õ�P�������ʾΪ��![]() ����m��n������֪
����m��n������֪![]() ����x1��y1����
����x1��y1����![]() ����x2��y2�������x1x2+y1y2��0����ô
����x2��y2�������x1x2+y1y2��0����ô![]() ��
��![]() ���ഹֱ�����������������У����ഹֱ���ǣ�������
���ഹֱ�����������������У����ഹֱ���ǣ�������
A.![]() ����3��20190����
����3��20190����![]() ������3��1��1��
������3��1��1��
B.![]() ����
����![]() ��1��1����
��1��1����![]() ����
����![]() +1��1��
+1��1��
C.![]() ����
����![]() ����
����![]() ��������
��������![]() ��2��8��
��2��8��
D.![]() ����
����![]() +2��
+2��![]() ����
����![]() ����
����![]() ��2��
��2��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4.�����ȡһ��С��Ȼ��Żأ����������һ��С��������״ͼ���б����������¼��ĸ���.
��1������ȡ����С��ı����ͬ��
��2������ȡ����С���ŵĺ͵���6.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
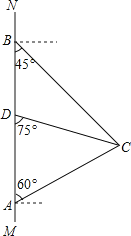
����Ŀ����ͼ�����ϱ�����ĺ�����![]() �ϣ���
�ϣ���![]() ����Ѳ�ߴ����־��յ����ϴ�
����Ѳ�ߴ����־��յ����ϴ�![]() ������źţ���֪
������źţ���֪![]() �������
�������![]() �����
�����![]() �ڴ�
�ڴ�![]() �ı�ƫ��60�㷽���ϣ���
�ı�ƫ��60�㷽���ϣ���![]() �ڴ�
�ڴ�![]() �Ķ��Ϸ����ϣ�
�Ķ��Ϸ����ϣ� ![]() ����һ�۲��
����һ�۲��![]() ����ô�
����ô�![]() �����ڹ۲��
�����ڹ۲��![]() ����ƫ��75�㷽���ϣ�
����ƫ��75�㷽���ϣ�
��1���ֱ����![]() ��
��![]() ��
��![]() ��
��![]() ��ľ���
��ľ���![]() ��
��![]() �� (��������и��ţ�����뱣������) (����ʾ�����������:��
�� (��������и��ţ�����뱣������) (����ʾ�����������:��![]() ����
����![]() )
)
(2)��֪��۲��![]() ��100���ﷶΧ���а�������Ѳ�ߴ�
��100���ﷶΧ���а�������Ѳ�ߴ�![]() ��ֱ��
��ֱ��![]() ȥӪ�ȴ�
ȥӪ�ȴ�![]() ��ȥӪ�ȵ�;����������Σ��?(�ο�����:
��ȥӪ�ȵ�;����������Σ��?(�ο�����: ![]() )
)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com