
����Ŀ���ڡ�ABC�У���ACB��90�㣬BC��kAC����D��AC�ϣ�����BD��
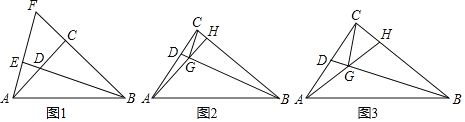
��1����ͼ1����k��1ʱ��BD���ӳ��ߴ�ֱ��AE������ΪE���ӳ�BC��AE���ڵ�F����֤��CD��CF��
��2������C��CG��BD������ΪG������AG���ӳ���BC�ڵ�H��
����ͼ2����CH��![]() CD��̽���߶�AG��GH��������ϵ���ú�k�Ĵ���ʽ��ʾ������֤����
CD��̽���߶�AG��GH��������ϵ���ú�k�Ĵ���ʽ��ʾ������֤����
����ͼ3������D��AC���е㣬ֱ��д��cos��CGH��ֵ���ú�k�Ĵ���ʽ��ʾ����
���𰸡���1��֤������������2����![]() ��֤������������cos��CGH=
��֤������������cos��CGH=![]() ��
��
��������
��1��ֻҪ֤����ACF�ա�BCD��ASA���������Ƴ�CF��CD��
��2�����ۣ�![]() ����CD��5a��CH��2a���������������ε��������AM��������ƽ���߷��߶γɱ����������ɽ�����⣮
����CD��5a��CH��2a���������������ε��������AM��������ƽ���߷��߶γɱ����������ɽ�����⣮
��3����ͼ3�У���AC��m����BC��km��![]() m����취֤����CGH����ABC���ɽ�����⣮
m����취֤����CGH����ABC���ɽ�����⣮
��1��֤������ͼ1�У�
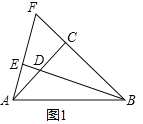
�ߡ�ACB��90�㣬BE��AF
���ACB����ACF����AEB��90��
�ߡ�ADE+��EAD����BDC+��DBC��90�㣬��ADE����BDC��
���CAF����DBC��
��BC��AC��
���ACF�ա�BCD��ASA����
��CF��CD��
��2���⣺���ۣ�![]() ��
��
���ɣ���ͼ2�У���AM��AC��CG���ӳ�����M��
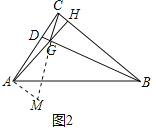
��CG��BD��MA��AC��
���CAM����CGD����BCD��90�㣬
���ACM+��CDG��90�㣬��ACM+��M��90�㣬
���CDB����M��
���BCD�ס�CAM��
��![]() ��k��
��k��
��CH��![]() CD����CD��5a��CH��2a��
CD����CD��5a��CH��2a��
��AM��![]() ��
��
��AM��CH��
��![]() ��
��
��![]() ��
��
��3���⣺��ͼ3�У���AC��m����BC��km��![]() m��
m��
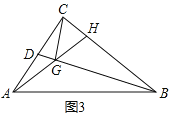
�ߡ�DCB��90�㣬CG��BD��
���DCG�ס�DBC��
��DC2��DGDB��
��AD��DC��
��AD2��DGDB��
��![]() ��
��
�ߡ�ADG����BDA��
���ADG�ס�BDA��
���DAG����DBA��
�ߡ�AGD����GAB+��DBA����GAB+��DAG����CAB��
�ߡ�AGD+��CGH��90�㣬��CAB+��ABC��90�㣬
���CGH����ABC��
��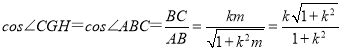 .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2+��2m��1��x��2m��m��0.5������͵��������Ϊ��4��

��1���������ߵĽ���ʽ��
��2����ͼ1����������x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��DΪ�������ϵ�һ�㣬BDƽ���ı���ABCD����������D�����ꣻ
��3����ͼ2��ƽ��������y��x2+��2m��1��x��2m��ʹ�䶥��Ϊ����ԭ�㣬ֱ��y����2����һ����P������P������ֱ�ߣ��ֱ�����������Ψһ�Ĺ�����E��F��ֱ��PE��PF����y��ƽ�У�����֤��ֱ��EF���ijһ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
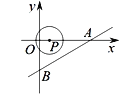
����Ŀ����ͼ��ֱ��![]() ��x���ڵ�A����y���ڵ�B����P��x����һ���㣬�Ե�PΪԲ�ģ���1����λ����Ϊ�뾶����P������P��ֱ��AB����ʱ����P�ĺ�������_____
��x���ڵ�A����y���ڵ�B����P��x����һ���㣬�Ե�PΪԲ�ģ���1����λ����Ϊ�뾶����P������P��ֱ��AB����ʱ����P�ĺ�������_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y��ax2+bx+c��ͼ��������˵����������ȷ���У�������
��ac��0��
��2a+b��0��
��4ac��b2��
��a+b+c��0��
����x��0ʱ��y��x���������С��
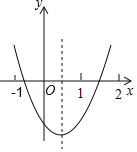
A.5��B.4��C.3��D.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
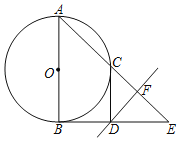
����Ŀ����ͼ����Rt��ABE�У���B��90�㣬��ABΪֱ������O��AE�ڵ�C��CE�Ĵ�ֱƽ����FD��BE�ڵ�D������CD��
��1���ж�CD����O��λ�ù�ϵ����֤����
��2����AC��6��CE��8������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ�Ķ��κ���y=ax2+bx+c��a��0����ͼ���У��۲�ó�������������Ϣ��
��ab��0����a+b+c��0����b+2c��0����a��2b+4c��0����![]() ��
��
����Ϊ������ȷ��Ϣ�ĸ�����

A��2�� B��3�� C��4�� D��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ǡ�O���һ�㣬CB���O�����ڵ�B��AC����O�ڵ�D����E��![]() �ϵ�һ�㣨�����A��B��D�غϣ�������C��48�������AED�Ķ���Ϊ_____��
�ϵ�һ�㣨�����A��B��D�غϣ�������C��48�������AED�Ķ���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�������������
2����4��8����16��32����64����
4����2��10����14��34����62����
��1��2����4��8����16��32����
�������������ĵ�n���У��������µ��������ֱ��Ϊa��b��c���۲���Щ�����ص㣬���������õ��Ĺ��ɣ��������Ϊ���⣮
��1���ú�n��ʽ�ӷֱ��ʾ��a��b��c��
��2�����ݣ�1���Ľ��ۣ���a��b��c�������ĺ�Ϊ770����n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ������ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ1��2��3��4.�����ȡһ��С��Ȼ��Żأ����������һ��С��������״ͼ���б����������¼��ĸ���.
��1������ȡ����С��ı����ͬ��
��2������ȡ����С���ŵĺ͵���6.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com