
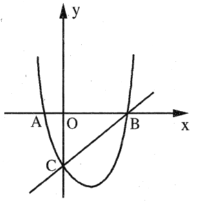
【题目】如图,二次函数的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() 是直线
是直线![]() 下方抛物线上一动点.
下方抛物线上一动点.
(1)求这个二次函数的表达式;
(2)连接![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 面积最大,若存在,求出点
面积最大,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() ,使
,使![]() 面积最大,点
面积最大,点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
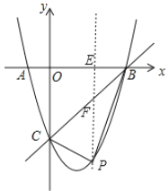
(2)过P作PE⊥x轴,交x轴于点E,交直线BC于点F,用P点坐标可表示出PF的长,则可表示出△PBC的面积,利用二次函数的性质可求得△PBC面积的最大值及P点的坐标.
(1)∵二次函数的图象交![]() 轴于点
轴于点![]() ,
,
∴设二次函数表达式为![]() ,
,
把A、B二点坐标代入可得![]() ,
,
解这个方程组,得![]() ,
,
∴抛物线解析式为:![]() ;
;
(2))∵点P在抛物线上,
∴设点![]() 的坐标为
的坐标为![]()
过![]() 作
作![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]()
设直线![]() 的函数表达式
的函数表达式![]() ,
,
将B(4,0),C(0,-4)代入得![]() ,
,
解这个方程组,得![]() ,
,
∴直线BC解析式为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]()
![]() ,
,
∵![]() ,
,
![]() 当
当![]() 时,
时,![]() 最大,
最大,
此时![]() ,
,
所以存在点![]() ,使
,使![]() 面积最大,点
面积最大,点![]() 的坐标为
的坐标为![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标和纵坐标相等的点叫“梦之点”,例如点(1,1),(﹣2,﹣2),![]() ,…都是“梦之点”,显然“梦之点”有无数个.
,…都是“梦之点”,显然“梦之点”有无数个.
(1)若点P(2,m)是反比例函数y=![]() (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s﹣1(k,s为常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标,若不存在,说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣b+![]() ,试求t的取值范围.
,试求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.

(1)求抛物线的解析式;
(2)如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;
(3)如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为4,点O是△ABC的外心,∠FOG=120°.绕点O旋转∠FOG,分别交线段AB、BC于D、E两点.连接DE给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③S四边形ODBE=![]() ;④△BDE周长的最小值为6.上述结论中正确的个数是( )
;④△BDE周长的最小值为6.上述结论中正确的个数是( )
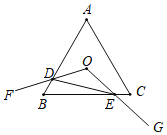
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
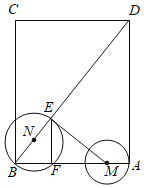
【题目】如图,在矩形ABCD中,AB=3,BC=4,半径为1的动圆圆心M从A点出发,沿着AB方向以1个单位长度/每秒的速度匀速运动,同时动点N从点B出发,沿着BD方向也以1个单位长度/每秒的速度匀速运动,设运动的时间为t秒(0≤t≤2.5),以点N为圆心,NB的长为半径的⊙N与BD,AB的交点分别为E,F,连结EF,ME.
(1)①当t= 秒时,⊙N恰好经过点M;②在运动过程中,当⊙M与△ABD的边相切时,t= 秒;
(2)当⊙M经过点B时,①求N到AD的距离;②求⊙N被AD截得的弦长;
(3)若⊙N与线段ME只有一个公共点时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽台州”,我市某社区将辖区内一块不超过1000平方米的区域进行美化.经调查,美化面积为100平方米时,每平方米的费用为300元.每增加1平方米,每平方米的费用下降0.2元。设美化面积增加x平方米,美化所需总费用为y元.
(1)求y与x的函数关系式;
(2)当美化面积增加100平方米时,美化的总费用为多少元;
(3)当美化面积增加多少平方米时,美化所需费用最高?最高费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
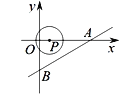
【题目】如图,直线![]() 交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的横坐标是_____
交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的横坐标是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,对于下列说法:其中正确的有( )
①ac>0,
②2a+b>0,
③4ac<b2,
④a+b+c<0,
⑤当x>0时,y随x的增大而减小,
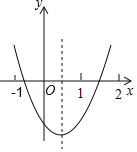
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
2,﹣4,8,﹣16,32,﹣64,…
4,﹣2,10,﹣14,34,﹣62,…
﹣1,2,﹣4,8,﹣16,32,…
在上面三行数的第n列中,从上往下的三个数分别记为a,b,c,观察这些数的特点,根据你所得到的规律,解答下列为问题.
(1)用含n的式子分别表示出a,b,c;
(2)根据(1)的结论,若a,b,c三个数的和为770,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com