
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E,连接OC.
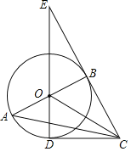
(1) 判断直线CD与⊙O的位置关系,并说明理由;
(2) 若BE=![]() ,DE=3,求⊙O的半径及AC的长.
,DE=3,求⊙O的半径及AC的长.
【答案】(1)DC是⊙O的切线,理由见解析;(2)半径为1,AC=![]()
【解析】
(1)欲证明CD是切线,只要证明OD⊥CD,利用全等三角形的性质即可证明;
(2)设⊙O的半径为r.在Rt△OBE中,根据OE2=EB2+OB2,可得![]() ,推出r=1,可得OE=2,即有
,推出r=1,可得OE=2,即有![]() ,可推出
,可推出![]() ,则利用勾股定理和含有30°的直角三角形的性质,可求得OC=2,
,则利用勾股定理和含有30°的直角三角形的性质,可求得OC=2,![]() ,再利用勾股定理求出
,再利用勾股定理求出![]() 即可解决问题;
即可解决问题;
(1)证明:∵CB=CD,CO=CO,OB=OD,
∴△OCB≌△OCD(SSS),
∴∠ODC=∠OBC=90°,
∴OD⊥DC,
∴DC是⊙O的切线;
(2)解: 设⊙O的半径为r.
在Rt△OBE中,∵OE2=EB2+OB2,
∴![]() ,
,
∴![]()
∴OE=3-1=2
Rt△ABC中,![]()
∴![]()
∴![]()
![]()
Rt△BCO中,![]() ,
,
![]()
Rt△ABC中,![]()


科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量![]() (毫克/百毫升)与时间
(毫克/百毫升)与时间![]() (时)成正比例;1.5小时后(包括1.5小时)
(时)成正比例;1.5小时后(包括1.5小时)![]() 与
与![]() 成反比例。根据图中提供的信息,解答下列问题:
成反比例。根据图中提供的信息,解答下列问题:
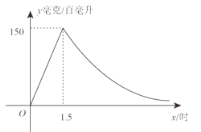
(1)请求出一般成人喝半斤低度白酒后,![]() 与
与![]() 之间的函数关系式及相应的自变量取值范围;
之间的函数关系式及相应的自变量取值范围;
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”不能驾车上路,参照上述数学模型,假设某驾驶员晚上21:00在家喝完半斤低度白酒,第二天最早几点驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
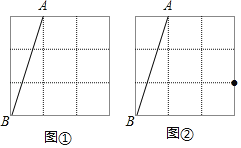
【题目】如图,在小正形的边长均为1的方格纸中,线段AB,点A,B均在小正方形的顶点上.
(1)在图①中画出平行四边形ABCD,且四边形ABCD的面积为6,点C、D均在小正方形的顶点上;
(2)在图②中画出一个△ABC,点C在小正方形的顶点上,且BC=BA,请直接写出∠BCA的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
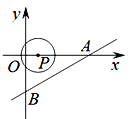
【题目】如图,直线![]() 交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是______________.
交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于二次函数的说法错误的是( )
A.抛物线y=﹣2x2+3x+1的对称轴是直线![]()
B.函数y=2x2+4x﹣3的图象的最低点在(﹣1,﹣5)
C.二次函数y=(x+2)2+2的顶点坐标是(﹣2,2)
D.点A(3,0)不在抛物线y=x2﹣2x﹣3上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 经过点
经过点![]() ,且满足9a+3b+c<0,以下结论:①a+b<0;②4a+c<0;③对于任何x,都有
,且满足9a+3b+c<0,以下结论:①a+b<0;②4a+c<0;③对于任何x,都有![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张准备给长方形客厅铺设瓷砖,已知客厅长AB=8m,宽BC=6m,现将其划分成一个长方形EFGH区域I和环形区域Ⅱ,区域Ⅰ用甲、乙瓷砖铺设,其中甲瓷砖铺设成的是两个全等的菱形图案,区域Ⅱ用丙瓷砖铺设,如图所示,已知N是GH中点,点M在边HE上,HN=3HM,设HM=x(m).
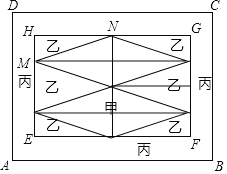
(1)用含x的代数式表示以下数量.铺设甲瓷砖的面积为 m2,铺设丙瓷砖的面积为 m2.
(2)若甲、乙、丙瓷砖单价分别为300元/m2,200元/m2,100元/m2,且EF≥FG+2,铺设好整个客厅,三种瓷砖总价至少需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)从袋中任意摸出一球,放回摇匀后,再摸出一球,则两次都摸到白球的概率是多少?请你用列表或画树状图的方法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com