
【题目】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:
(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)结合你的示意图,写出求电线杆高度的思路.
【答案】
(1)解:测量方案示意图如图;选用的测量工具:高为1.5m的测角仪,皮尺;

(2)解:CA(测角仪离电线杆的距离)=a,DC测角仪的高=1.5m,∠BDE(测角仪测的仰角)=α,
根据正切函数;可得:tanα= ![]() ;
;
因为DE=CA=a(m),AE=CD=1.5m,
即BE=tanαa(m),
则AB=BE+AE=(tanαa+1.5)m.
故电线杆高度为(tanαa+1.5)米
【解析】(1)先根据已知的测量工具画出测量方案示意图,测量工具为高为1.5m的测角仪、皮尺。
(2)根据设计测量的方法,先测得AC的长、∠BDE的度数,根据矩形的性质得出DE=CA、AE=CD,再根据锐角三角函数的正切函数的定义,求出BE的长,再根据AB=BE+AE,即可求得结果。
【考点精析】利用锐角三角函数的定义对题目进行判断即可得到答案,需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:
(1)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动_____个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,运动t秒钟过后:
①点A、B、C表示的数分别是_____、_____、_____ (用含t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2.试问:d1﹣d2的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求出d1﹣d2值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A,点B,点C表示的数分别为﹣2,1,6.
![]()
(1)线段AB的长度为 个单位长度,线段AC的长度为 个单位长度.
(2)点P是数轴上的一个动点,从A点出发,以每秒1个单位长度的速度,沿数轴的正方向运动,运动时间为t秒(0≤t≤8).用含t的代数式表示:线段BP的长为 个单位长度,点P在数轴上表示的数为 ;
(3)点M,点N都是数轴上的动点,点M从点A出发以每秒4个单位长度的速度运动,点N从点C出发以每秒3个单位长度的速度运动.设点M,N同时出发,运动时间为x秒.点M,N相向运动,当点M,N两点间的距离为13个单位长度时,求x的值,并直接写出此时点M在数轴上表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]()
(2)计算:3a(2a2-9a+3)-4a(2a-1)
(3)计算:(![]() )×(
)×(![]() )+|
)+|![]() -1|+(5-2π)0
-1|+(5-2π)0
(4)先化简,再求值:(xy2+x2y)![]() ,其中x=
,其中x=![]() ,y=
,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
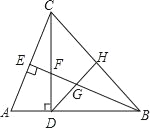
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )
(1)△ABC是等腰三角形;(2)BF=AC;(3)BH:BD:BC=1:![]() :
:![]() ;(4)GE2+CE2=BG2.
;(4)GE2+CE2=BG2.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,从边长为a的正方形纸片中减去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形(其面积= ![]() ).
).
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a、b的式子表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度.
图1为点P在⊙O外的情形示意图.
(1)若点B(1,0),C(1,1),D(0, ![]() ),则SB=;SC=;SD=;
),则SB=;SC=;SD=;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR , 直接写出满足条件的线段PQ长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com