
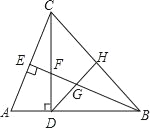
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )
(1)△ABC是等腰三角形;(2)BF=AC;(3)BH:BD:BC=1:![]() :
:![]() ;(4)GE2+CE2=BG2.
;(4)GE2+CE2=BG2.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
(1)根据角平分线的定义可得∠ABE=∠CBE,根据等角的余角相等求出∠A=∠BCA,再根据等角对等边可得AB=BC,从而得证;
(2)根据三角形的内角和定理求出∠A=∠DFB,推出BD=DC,根据AAS证出△BDF≌△CDA即可;
(3)根据等腰直角三角形斜边上的中线等于斜边的一半进行解答;
(4)由(2)得出BF=AC,再由BF平分∠DBC和BE⊥AC通过ASA证得△ABE≌△CBE,即得CE=AE=![]() AC,连接CG,由H是BC边的中点和等腰直角三角形△DBC得出BG=CG,再由直角△CEG得出CG2=CE2+GE2,从而得出CE,GE,BG的关系.
AC,连接CG,由H是BC边的中点和等腰直角三角形△DBC得出BG=CG,再由直角△CEG得出CG2=CE2+GE2,从而得出CE,GE,BG的关系.
解:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵CD⊥AB,
∴∠ABE+∠A=90°,∠CBE+∠ACB=90°,
∴∠A=∠BCA,
∴AB=BC,
∴△ABC是等腰三角形;
故(1)正确;
(2)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°﹣45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中
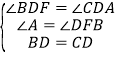 ,
,
∴△BDF≌△CDA(AAS),
∴BF=AC;
故(2)正确;
(3)∵在△BCD中,∠CDB=90°,∠DBC=45°,
∴∠DCB=45°,
∴BD=CD,BC=![]() BD.
BD.
由点H是BC的中点,
∴DH=BH=CH=![]() BC,
BC,
∴BD=![]() BH,
BH,
∴BH:BD:BC=BH:![]() BH:2BH=1:
BH:2BH=1:![]() :2.
:2.
故(3)错误;
(4)由(2)知:BF=AC,
∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE⊥AC,
∴∠AEB=∠CEB,
在△ABE与△CBE中,
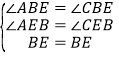 ,
,
∴△ABE≌△CBE(AAS),
∴CE=AE=![]() AC,
AC,
∴CE=![]() AC=
AC=![]() BF;
BF;
连接CG.
∵BD=CD,H是BC边的中点,
∴DH是BC的中垂线,
∴BG=CG,
在Rt△CGE中有:CG2=CE2+GE2,
∴CE2+GE2=BG2.
故(4)正确.
综上所述,正确的结论由3个.
故选:C.


科目:初中数学 来源: 题型:
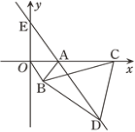
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边三角形△CBD,连接DA并延长,交y轴于点E.
(1)求证:△OBC≌△ABD
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化,请说明理由.
(3)当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= ![]() 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.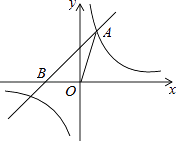
(1)求k和b的值;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
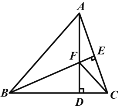
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:
(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)结合你的示意图,写出求电线杆高度的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索研究:已知:△ABC和△CDE都是等边三角形.
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为: ,线段AD与BE所成的锐角度数为 °;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.
(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com