
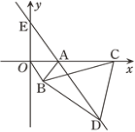
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边三角形△CBD,连接DA并延长,交y轴于点E.
(1)求证:△OBC≌△ABD
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化,请说明理由.
(3)当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?
【答案】(1)证明见解析;(2)在点C的运动过程中,∠CAD的度数不会变化,理由见解析;(3) 当点C运动到(3,0)时,以A,E,C为顶点的三角形是等腰三角形.
【解析】
(1)先根据等边三角形的性质得∠OBA=∠CBD=60°,OB=BA,BC=BD,则∠OBC=∠ABD,然后可根据“SAS”可判定△OBC≌△ABD;
(2)根据等边三角形的性质即可得出;
(3)先根据全等三角形的性质以及等边三角形的性质,求得∠EAC=120°,进而得出以A,E,C为顶点的三角形是等腰三角形时,AE和AC是腰,最后根据Rt△AOE中,OA=1,∠OEA=30°,求得AC=AE=2,据此得到OC=1+2=3,即可得出点C的位置.
(1)证明:∵△AOB、△CBD都是等边三角形
∴ BO=BA,BC=BD, ∠OBA=∠CBD=600
∴ ∠OBA+∠ABC = ∠CBD+∠ABC
∴ ∠OBC = ∠ABD
∴ △OBC≌△ABD
(2)解:在点C的运动过程中,∠CAD的度数不会变化,理由如下:
∵ △AOB是等边三角形
∴ ∠BOA =∠OAB= 60°
∵ △OBC≌△ABD
∴ ∠BAD =∠BOC= 60°
∴ ∠CAD=1800-∠0AB-∠BAD= 60°
(3)解:∵ A(1,0)
∴ OA=1
∵ ∠EOA= 900,∠EAO=∠CAD= 60°
∴ ∠OEA= 30°
∴ AE=2OA=2
∵ ∠EAC=180°-∠EAO=120°
∴ 当以A,E,C为顶点的三角形是等腰三角形时,AE、AC是腰
∴ AE=AC=2
∴ OC=OA+AC=3
∴ 当点C运动到(3,0)时,以A,E,C为顶点的三角形是等腰三角形.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 在数轴上表示的数是-8,点
在数轴上表示的数是-8,点![]() 在数轴上表示的数是16.若点
在数轴上表示的数是16.若点![]() 以6个单位长度/秒的速度向右匀速运动,同时点
以6个单位长度/秒的速度向右匀速运动,同时点![]() 以2个单位长度/秒的速度向左匀速运动.问:当
以2个单位长度/秒的速度向左匀速运动.问:当![]() 时,运动时间为多少秒?
时,运动时间为多少秒?
![]()
A. 2秒B. 13.4秒C. 2秒或4秒D. 2秒或6秒
查看答案和解析>>
科目:初中数学 来源: 题型:
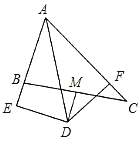
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线MD相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③DM平分∠ADF;④AB+AC=2AE.其中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车每千米耗油0.2升,这次共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:
(1)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动_____个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,运动t秒钟过后:
①点A、B、C表示的数分别是_____、_____、_____ (用含t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2.试问:d1﹣d2的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求出d1﹣d2值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b与x轴,y轴分别交于A,B两点,且经过点(4,b+3).
(1)求k的值;
(2)若AB=OB+2,
①求b的值;
②点M为x轴上一动点,点N为坐标平面内另一点.若以A,B,M,N为顶点的四边形是菱形,请直接写出所有符合条件的点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
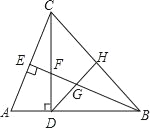
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )
(1)△ABC是等腰三角形;(2)BF=AC;(3)BH:BD:BC=1:![]() :
:![]() ;(4)GE2+CE2=BG2.
;(4)GE2+CE2=BG2.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com