
【题目】解决问题:
一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.
(2)小明家距小彬家多远?
(3)货车每千米耗油0.2升,这次共耗油多少升?
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。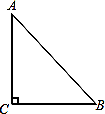
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王华在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第31页遇到这样一道题:
如图1,在△ABC中,P是边AB上的一点,联结CP.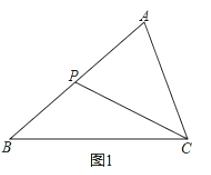
要使△ACP∽△ABC,还需要补充的一个条件是__,或__.
(1)王华补充的条件是 , 或 .
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2= AB2+AB.BC.
求∠C的度数.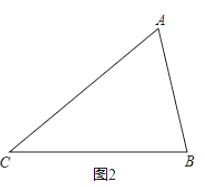
查看答案和解析>>
科目:初中数学 来源: 题型:
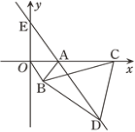
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边三角形△CBD,连接DA并延长,交y轴于点E.
(1)求证:△OBC≌△ABD
(2)在点C的运动过程中,∠CAD的度数是否会变化?如果不变,请求出∠CAD的度数;如果变化,请说明理由.
(3)当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(2﹣π)0+(![]() )﹣2+(﹣2)3
)﹣2+(﹣2)3
(2)(﹣3a6)2﹣a22a10+(﹣2a2)3a3
(3)(x+1)2﹣(1﹣2x)(1+2x)
(4)(x+2)(x﹣3)﹣x(x+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
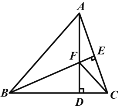
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=2,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com