
【题目】如图,在四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() .
.
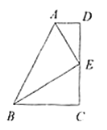
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为______(直接写出结果).
的面积为______(直接写出结果).
【答案】(1)证明见解析;(2)证明见解析;(3)24.
【解析】
(1)由平行线的性质可得∠BAD+∠ABC=180°,由角平分线的性质可得∠DAE=∠BAE=![]() ∠BAD,∠ABE=∠CBE=
∠BAD,∠ABE=∠CBE=![]() ∠ABC,可求得∠BEA=90°,即可得结论;
∠ABC,可求得∠BEA=90°,即可得结论;
(2)延长AE,BC交于点F,由平行线的性质可得∠DAE=∠F=∠BAE,可得AB=BF,由等腰三角形的性质可得AE=EF,由“ASA”可证△ADE≌△FCE,可得AD=CF,即可得结论;
(3)由全等三角形的性质可得S△ADE=S△FCE,可得S四边形ABCD=S△ABF,由三角形面积公式可求解.
证明:(1)∵AD∥BC,
∴![]() ,
,
又![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
∴∠DAE=∠BAE=![]() ∠BAD,∠ABE=∠CBE=
∠BAD,∠ABE=∠CBE=![]() ∠ABC,
∠ABC,
∴![]() ,
,
∴∠BEA=90°,
∴![]() ;
;
(2)延长AE,BC交于点F,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵∠DAE=∠F,∠AED=∠FEC,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3))∵AE=4,
∴EF=4,
∴AF=8,
∵△ADE≌△FCE,
∴S△ADE=S△FCE,
∴S四边形ABCD=S△ABF,
∴S四边形ABCD=![]() AF×BE=24,
AF×BE=24,
故答案为:24.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,连接EF交AD于G,下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,△AEF是等边三角形,其中正确的结论的个数为( )
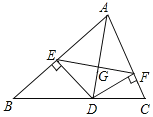
A.2B.3C.4D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(如图,△ABC 中,AB=AC,以 AB 为直径的 ![]() O 与 BC 相交于点 D,与 CA 的延长线相交于点 E,过点 D 作 DF⊥AC 于 F.
O 与 BC 相交于点 D,与 CA 的延长线相交于点 E,过点 D 作 DF⊥AC 于 F.

(1)求证:DF 是 ⊙O 的切线;
(2)若 AC=3AE,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

查看答案和解析>>
科目:初中数学 来源: 题型:
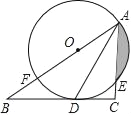
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在中秋节来临前夕,购进一种品牌月饼,每盒进价是![]() 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于![]() 元.根据以往销售经验发现;当售价定为每盒
元.根据以往销售经验发现;当售价定为每盒![]() 元时,每天可以卖出
元时,每天可以卖出![]() 盒,每盒售价每提高
盒,每盒售价每提高![]() 元,每天要少卖出
元,每天要少卖出![]() 盒.
盒.
![]() 当每盒售价定为多少元时,每天销售的利润
当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
![]() 为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于
为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于![]() 元.如果超市想要每天获得
元.如果超市想要每天获得![]() 元的利润,那么超市每天销售月饼多少盒?
元的利润,那么超市每天销售月饼多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的表达式为![]() .
.
![]() 求此抛物线与
求此抛物线与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
![]() 求抛物线与坐标轴围成的三角形的面积;
求抛物线与坐标轴围成的三角形的面积;
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com