
【题目】为满足市场需求,某超市在中秋节来临前夕,购进一种品牌月饼,每盒进价是![]() 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于![]() 元.根据以往销售经验发现;当售价定为每盒
元.根据以往销售经验发现;当售价定为每盒![]() 元时,每天可以卖出
元时,每天可以卖出![]() 盒,每盒售价每提高
盒,每盒售价每提高![]() 元,每天要少卖出
元,每天要少卖出![]() 盒.
盒.
![]() 当每盒售价定为多少元时,每天销售的利润
当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
![]() 为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于
为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于![]() 元.如果超市想要每天获得
元.如果超市想要每天获得![]() 元的利润,那么超市每天销售月饼多少盒?
元的利润,那么超市每天销售月饼多少盒?
【答案】(1)当每盒定价为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(2)如果超市想要每天获得![]() 元的利润,那么超市每天销售月饼
元的利润,那么超市每天销售月饼![]() 盒.
盒.
【解析】
(1)根据“当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒”即可得出每天的销售量与每盒售价x(元)之间的函数关系式,然后根据利润=1盒粽子所获得的利润×销售量列式整理,再进行配方从而可求得答案;
(2)先由(1)中所求得的P与x的函数关系式,根据这种粽子的每盒售价不得高于58元,且每天销售粽子的利润等于6000元,求出x的值,再根据(1)中所求得的销售量与每盒售价x(元)之间的函数关系式即可求解.
解:(1)由题意得销售量=700-20(x-45)=-20x+1600,
P=(x-40)(-20x+1600) =-20x2+2400x-64000=-20(x-60)2+8000,
∵x≥45,a=-20<0,
∴当x=60时,P最大值=8000元
即当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(2)由题意,得-20(x-60)2+8000=6000,
解得x1=50,x2=70.
∵每盒售价不得高于58元,
∴x2=70(舍去),
∴-20×50+1600=600(盒).
答:如果超市想要每天获得6000元的利润,那么超市每天销售月饼600盒.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )
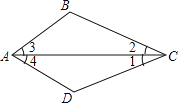
A.AB=AD,∠2=∠1
B.AB=AD,∠3=∠4
C.∠2=∠1,∠3=∠4
D.∠2=∠1,∠B=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论: ①abc<0②2a+b=0③当x=﹣1或x=3时,函数y的值都等于0.④4a+2b+c<0,其中正确结论的个数是( )
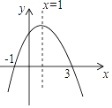
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 的平分线
的平分线![]() 和
和![]() 的外角平分线
的外角平分线![]() 相交于点
相交于点![]() ,分别交
,分别交![]() 和
和![]() 的延长线于
的延长线于![]() ,
,![]() .过
.过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论有( )
;其中正确的结论有( )
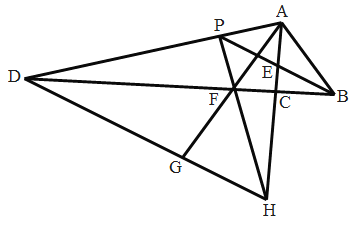
A.4个B.3个C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)[x(x2-2x+3)-3x]÷![]() x2;
x2;
(2)x(4x+3y)-(2x+y)(2x-y);
(3)5a2b÷![]() ·(2ab2)2;
·(2ab2)2;
(4)(a-2b-3c)(a-2b+3c).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
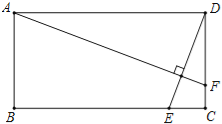
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)当CF=1时,求EC的长.
(3)若直线AF与线段BC延长线交于点G,当△DBE与△DFG相似时,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂研制一种新产品并投放市场,根据市场调查的信息得出这种新产品的日销产量y(万件)与销售的天数x(天)的关系如图所示.根据图像按下列要求作出
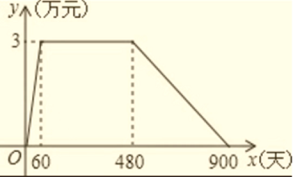
(1)求开始时,不断上升的日销售量y(万件)与销售天数x(天)的函数关系式;
(2)已知销售一件产品获利0.9元,求在该产品日销量不变期间的利润有多少万元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com