
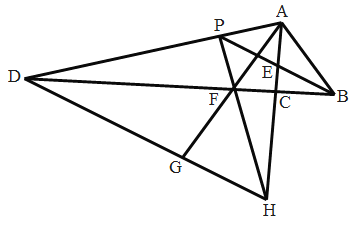
【题目】如图,![]() 中,
中,![]() ,
,![]() 的平分线
的平分线![]() 和
和![]() 的外角平分线
的外角平分线![]() 相交于点
相交于点![]() ,分别交
,分别交![]() 和
和![]() 的延长线于
的延长线于![]() ,
,![]() .过
.过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论有( )
;其中正确的结论有( )
A.4个B.3个C.
【答案】A
【解析】
①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP,再根据角平分线的定义∠ABP=![]() ∠ABC,然后利用三角形的内角和定理整理即可得解;
∠ABC,然后利用三角形的内角和定理整理即可得解;
②先求出∠APB=∠FPB,再利用“角边角”证明△ABP和△FBP全等,根据全等三角形对应边相等得到AB=BF,AP=PF;
③根据直角的关系求出∠AHP=∠FDP,然后利用“角角边”证明△AHP与△FDP全等,根据全等三角形对应边相等可得DF=AH;
④求出∠ADG=∠DAG=45°,再根据等角对等边可得DG=AG,再根据等腰直角三角形两腰相等可得GH=GF,然后根据FG=GH,AF=![]() 即可得到
即可得到![]() .
.
解:①∵∠ABC的角平分线BE和∠BAC的外角平分线,
∴∠ABP=![]() ∠ABC,
∠ABC,
∠CAP=![]() (90°+∠ABC)=45°+
(90°+∠ABC)=45°+![]() ∠ABC,
∠ABC,
在△ABP中,∠APB=180°∠BAP∠ABP,
=180°(45°+![]() ∠ABC+90°∠ABC)
∠ABC+90°∠ABC)![]() ∠ABC,
∠ABC,
=180°45°![]() ∠ABC90°+∠ABC
∠ABC90°+∠ABC![]() ∠ABC,
∠ABC,
=45°,故本小题正确;
②∵PF⊥AD,∠APB=45°(已证),
∴∠APB=∠FPB=45°,
∵∵PB为∠ABC的角平分线,
∴∠ABP=∠FBP,
在△ABP和△FBP中,
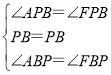 ,
,
∴△ABP≌△FBP(ASA),
∴AB=BF,AP=PF;
∴![]() 垂直平分
垂直平分![]() ,故②正确;
,故②正确;
③∵∠ACB=90°,PF⊥AD,
∴∠FDP+∠HAP=90°,∠AHP+∠HAP=90°,
∴∠AHP=∠FDP,
∵PF⊥AD,
∴∠APH=∠FPD=90°,
在△AHP与△FDP中,
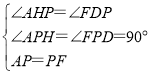 ,
,
∴△AHP≌△FDP(AAS),
∴DF=AH,
∵BD=DF+BF,
∴BD=AH+AB,
∴BDAH=AB,故③小题正确;
④∵AP=PF,PF⊥AD,
∴∠PAF=45°,
∴∠ADG=∠DAG=45°,
∴DG=AG,
∵∠PAF=45°,AG⊥DH,
∴△ADG与△FGH都是等腰直角三角形,
∴DG=AG,GH=GF,
∴DG=GH+AF,
∴FG=GH,AF=![]()
故![]() .
.
综上所述①②③④正确.
故选:A.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
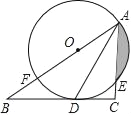
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.

(1)求证:△ABD≌△ACD.
(2)求∠ADE的度数.
(3)试猜想线段DE,AD,DC之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在中秋节来临前夕,购进一种品牌月饼,每盒进价是![]() 元.超市规定每盒售价不得少于
元.超市规定每盒售价不得少于![]() 元.根据以往销售经验发现;当售价定为每盒
元.根据以往销售经验发现;当售价定为每盒![]() 元时,每天可以卖出
元时,每天可以卖出![]() 盒,每盒售价每提高
盒,每盒售价每提高![]() 元,每天要少卖出
元,每天要少卖出![]() 盒.
盒.
![]() 当每盒售价定为多少元时,每天销售的利润
当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
![]() 为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于
为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于![]() 元.如果超市想要每天获得
元.如果超市想要每天获得![]() 元的利润,那么超市每天销售月饼多少盒?
元的利润,那么超市每天销售月饼多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.

(1)当t=2时,求线段PQ的长度;
(2)当t为何值时,△PCQ的面积等于5cm2?
(3)在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
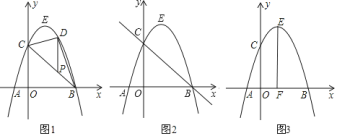
【题目】已知抛物线![]() 的图象经过点
的图象经过点![]() 、
、![]() ,顶点为
,顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的解析式和顶点
求抛物线的解析式和顶点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,
,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴平行线,交抛物线于点
轴平行线,交抛物线于点![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,若点
,若点![]() 是直线
是直线![]() 上的动点,点
上的动点,点![]() 、
、![]() 、
、![]() 所构成的三角形与
所构成的三角形与![]() 相似,请直接写出所有点
相似,请直接写出所有点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,
点,![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 是线段
是线段![]() 上一点,若
上一点,若![]() ,则
,则![]() 的最大值为________,最小值为________.
的最大值为________,最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+b的图象与直线y=x+2相交于点A(1,m)和点B(n,0).
(1)试确定二次函数的解析式;
(2)在给出的平面直角坐标系中画出这个函数图象的草图,并结合图象直接写出ax2+b>x+2时x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com