【题目】计算：
（1）[x(x2－2x＋3)－3x]÷
x2；
（2）x(4x＋3y)－(2x＋y)(2x－y)；
（3）5a2b÷
·(2ab2)2；
（4）(a－2b－3c)(a－2b＋3c)．
【答案】（1）2x－4；（2）3xy＋y2；（3）－60a3b4；（4）a2－4ab＋4b2－9c2.
【解析】
（1）先算括号，再算除法即可；
（2）先算乘法，再合并同类项即可．
（3）先算乘方，再算除法和乘法即可；
（4）先变形为[(a－2b)－3c][(a－2b)＋3c]，再按平方差公式计算即可．
解：（1）原式＝(x3－2x2＋3x－3x)÷
x2＝(x3－2x2)÷x2＝2x－4.
（2）原式＝4x2＋3xy－(4x2－y2)＝4x2＋3xy－4x2＋y2＝3xy＋y2.
（3）原式＝5a2b÷
·4a2b4＝－60a3b4.
（4）原式＝[(a－2b)－3c][(a－2b)＋3c]＝(a－2b)2－(3c)2＝a2－4ab＋4b2－9c2.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，∠BAC=120，AD⊥BC，且AD=AB．
（1）如图1，DE⊥AB，DF⊥AC，垂足分别为点E，F，求证：AE+AF=AD
（2）如图2，如果∠EDF=60，且∠EDF两边分别交边AB，AC于点E，F，那么线段AE，AF，AD之间有怎样的数量关系？并给出证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本小题满分8分）
如图，用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形，其中正五边形的边长为(
)
，正六边形的边长为(
)cm（其中
)，求这两段铁丝的总长
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形纸片ABCD中，已知AD =8，折叠纸片使AB边与对角线AC
重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )
A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为满足市场需求，某超市在中秋节来临前夕，购进一种品牌月饼，每盒进价是
元．超市规定每盒售价不得少于
元．根据以往销售经验发现；当售价定为每盒元时，每天可以卖出
盒，每盒售价每提高
元，每天要少卖出
盒．
当每盒售价定为多少元时，每天销售的利润
（元）最大？最大利润是多少？
为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于
元．如果超市想要每天获得
元的利润，那么超市每天销售月饼多少盒？
查看答案和解析>>
科目：初中数学 来源： 题型：
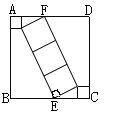
【题目】如图，在边长为7的正方形ABCD中放入五个小正方形后形成一个中心对称图形，其中两顶点E、F分别在边BC、AD上，则放入的五个小正方形的面积之和为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
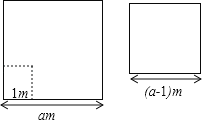
【题目】如图，“主收1号”小麦的试验田是边长为am(a＞1)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分，“丰收2号”小麦的试验田是边长为(a﹣1)m的正方形，两块试验田的小麦都收获了500kg.
(1)哪种小麦的单位面积产量高？
(2)若高的单位面积产量是低的单位面积产量的
(kg)倍，求a的值
(3)利用(2)中所求的a的值，分解因式x2﹣ax﹣108＝_____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天.
（1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？
（2）若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC中，AC=BC，∠C=120°，点D为AB边的中点，∠EDF=60°，DE、DF分别交AC、BC与E、F点。
（1）如图，若EF∥AB，求证DE=DF
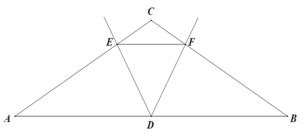
（2）如图，若EF与AB不平行，则问题（1）的结论是否成立？说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com