
【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3.
y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+![]() A)﹣(2b+
A)﹣(2b+![]() B)的值.
B)的值.
【答案】(1)(2b﹣2)x2﹣(a+3)x﹣(b+6);(2)﹣3![]() .
.
【解析】
(1)先化简原式,再分别代入A和B的表达式,去括号并合并类项即可;
(2)先代入A和B的表达式并去括号并合并类项,由题意可令x和x2项的系数为零,求解出a和b的数值,再化简原式后代入相关数值即可求解.
解:(1)∵A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3,
y﹣3,
∴原式=3A﹣4A+2B=﹣A+2B=﹣2x2﹣ax+5y﹣b+2bx2﹣3x﹣5y﹣6=(2b﹣2)x2﹣(a+3)x﹣(b+6);
(2)∵A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3,
y﹣3,
∴A﹣2B=2x2+ax﹣5y+b﹣2bx2+3x+5y+6=(2﹣2b)x2+(a+3)x+(b+6),
由x取任意数值时,A﹣2B的值是一个定值,得到2﹣2b=0,a+3=0,
解得:a=﹣3,b=1,
则原式=a﹣2b+![]() (A﹣2B)=﹣3﹣2+
(A﹣2B)=﹣3﹣2+![]() =﹣3
=﹣3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】通过学习,同学们已经体会到灵活运用乘法公式使整式的乘法运算方便、快捷.相信通过对下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.
例:用简便方法计算:![]() .
.
解:![]()
![]() ①
①
![]() ②
②
![]() .
.
(1)例题求解过程中,第②步变形是利用___________(填乘法公式的名称).
(2)用简便方法计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】做大小两个长方体纸盒,尺寸如下(单位:cm)

(1)做这两个纸盒共用料多少cm2?
(2)做大纸盒比做小纸盒多用料多少cm2?
(3)如果a=8,b=6,c=5,将24个小纸盒包装成一个长方体,这个长方体的表面积的最小值为________cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请在第三象限内画出△A2B2C2 , 并求出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点. 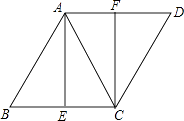
(1)求证:△ABE≌△CDF;
(2)若∠B=60°,AB=4,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三个点对应的数分别是a、b、c,满足|a+24|+|b+10|+(c﹣10)2=0;动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在返回过程中,当t=_____秒时,P、Q两点之间的距离为2.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列4个命题: ①方程x2﹣( ![]() +
+ ![]() )x+
)x+ ![]() =0的根是
=0的根是 ![]() 和
和 ![]() .
.
②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD= ![]() ,则CD=3.
,则CD=3.
③点P(x,y)的坐标x,y满足x2+y2+2x﹣2y+2=0,若点P也在y= ![]() 的图象上,则k=﹣1.
的图象上,则k=﹣1.
④若实数b、c满足1+b+c>0,1﹣b+c<0,则关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大的实数根x0满足﹣1<x0<1.
上述4个命题中,真命题的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0.
其中结论正确的是 . (填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2013年“崇左市初中毕业升学体育考试”测试中,参加男子掷实心球的10名考生的成绩记录如下(单位:米):7.5、6.5、8.2、7.8、8.8、8.2、8.6、8.2、8.5、9.5,则该组数据的众数、中位数、平均数依次分别是( )
A.8.2、8.0、7.5
B.8.2、8.5、8.1
C.8.2、8.2、8.15
D.8.2、8.2、8.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com