
【题目】做大小两个长方体纸盒,尺寸如下(单位:cm)

(1)做这两个纸盒共用料多少cm2?
(2)做大纸盒比做小纸盒多用料多少cm2?
(3)如果a=8,b=6,c=5,将24个小纸盒包装成一个长方体,这个长方体的表面积的最小值为________cm2.
【答案】(1)14ab+14bc+10ac;(2)10ab+10bc+6ac;(3)1936.
【解析】
(1)根据长方体表面积计算公式计算出两个长方体表面积,再相加化简可得;
(2)用大纸盒的用料减去做小纸盒的用料即可;
(3)根据已知条件求得结论即可.
(1)小纸盒用料:2ab+2bc+2ac;大纸盒用料:12ab+12bc+8ac.
两个纸盒共用料:(2ab+2bc+2ac)+(12ab+12bc+8ac)=14ab+14bc+10ac (cm2).
答:做这两个纸盒共用料(14ab+14bc+10ac)cm2.
(2)(12ab+12bc+8ac)﹣(2ab+2bc+2ac)=10ab+10bc+6ac.
答:做大纸盒比做小纸盒多用料(10ab+10bc+6ac)cm2.
(3)如果a=8,b=6,c=5,将24个小纸盒包装成一个长方体,这个长方体的表面积的最小值为2[(8×2×6×3+8×2×5×4+6×3×5×4)=1936(cm2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.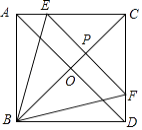
(1)求tan∠ABE的值.
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按下列要求作图(第(1)、(2)小题用尺规作图,第(3)小题不限作图工具,保留作图痕迹).
(1)作∠B的角平分线;
(2)作BC的中垂线;
(3)以BC边所在直线为对称轴,作△ABC的轴对称图形.
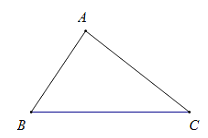
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE. 
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,P是线段AB上的任意一点,在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD,连结CD.
(1)当AP=6时,求CD的长;
(2)当AP为多少时,CD的值最小,最小值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3.
y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+![]() A)﹣(2b+
A)﹣(2b+![]() B)的值.
B)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容.图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2).线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1.求出点M的坐标并证明你的结论.
M( , )
证明:∵CA⊥AB,DB⊥AB
∴∠CAM=∠DBM=度.
∵CA=AM=3,DB=BM=2
∴∠ACM=∠AMC(),∠BDM=∠BMD(同理),
∴∠ACM= ![]() (180°﹣)=45°.∠BDM=45°(同理).
(180°﹣)=45°.∠BDM=45°(同理).
∴∠ACM=∠BDM
在△ACM与△BDM中,
∠CAM=∠DBM
∴△ACM∽△BDM(如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com