
【题目】如图,已知AB=10,P是线段AB上的任意一点,在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD,连结CD.
(1)当AP=6时,求CD的长;
(2)当AP为多少时,CD的值最小,最小值是多少?

【答案】(1)2![]() ;(2)当AP=5时,CD的长度最小,最小值是5.
;(2)当AP=5时,CD的长度最小,最小值是5.
【解析】
(1)如图,过C作CE⊥AB于E,过D作DF⊥PB于F,过D作DG⊥CE于G.即可得四边形DFEG为矩形.根据等边三角形的性质及矩形的性质求得EF=5,CG=![]() ,再利用勾股定理求得CD的长即可;(2)在(1)的基础上可得CD=
,再利用勾股定理求得CD的长即可;(2)在(1)的基础上可得CD=![]() ,当CG=0时,CD有最小值,由此求得CD的长即可.
,当CG=0时,CD有最小值,由此求得CD的长即可.
(1)如图,过C作CE⊥AB于E,过D作DF⊥PB于F,过D作DG⊥CE于G.即可得四边形DFEG为矩形.
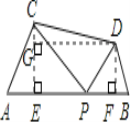
∵AB=10,AP=6,
∴PB=4,
∵△APC和△PBD是等边三角形,CE⊥AB , DF⊥PB,
∴EP=![]() AP=3,PF=
AP=3,PF=![]() PB=2,
PB=2,
∴EF=EP+FP=5.
在Rt△DPF中,DP=4,PF=2,
由勾股定理求得DF=![]() .
.
在Rt△CEP中,PC=6,PE=3,
由勾股定理求得CE=![]() .
.
由矩形的性质可得,DG=EF=5,EG=DF,
∴CG=![]() .
.
在Rt△CGD中,DG=5,CG=![]() ,由勾股定理求得CD=2
,由勾股定理求得CD=2![]() ;
;
(2)如图, 由(1)得,DG=EF=![]() AB=5,CD≥DG,
AB=5,CD≥DG,

∴CD=![]() ,故CG=0时,CD有最小值,
,故CG=0时,CD有最小值,
当P为AB中点时,有CD=DG=5,
所以CD长度的最小值是5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为提倡全民健身活动, 某社区准备购买羽毛球和羽毛球拍供社区居民使用, 某体育用品商店羽毛球每盒 10 元, 羽毛球拍每副 40 元 .该商店有两种优惠方案,方案一: 不购买会员卡时, 羽毛球享受 8.5 折优惠, 羽毛球拍购买 5 副(含5 副) 以上才能享受 8.5 折优惠, 5 副以下必须按定价购买;方案二: 每张会员卡 20 元, 办理会员卡时, 全部商品享受 8 折优惠 . 设该社区准备购买羽毛球拍 6 副, 羽毛球![]() 盒, 请回答下列问题:
盒, 请回答下列问题:
(1)如果一位体育爱好者按方案一只购买了 4 副羽毛球拍,求他购买时所需要的费用;
(2)用含![]() 的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
(3)①直接写出一个![]() 的值, 使方案一比方案二优惠;
的值, 使方案一比方案二优惠;
②直接写出一个![]() 的值, 使方案二比方案一优惠 .
的值, 使方案二比方案一优惠 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照有关规定:距高铁轨道 200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°.小王看中了①号楼A单元的一套住宅,与售楼人员的对话如下: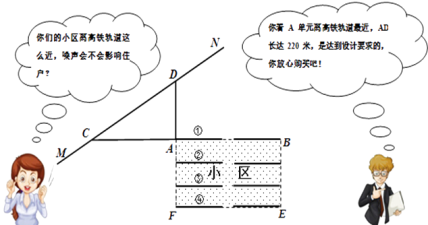
(1)小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
(2)若一列长度为228米的高铁以252千米/小时的速度通过时,则A单元用户受到影响时间有多长?
(温馨提示: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈6.1)
≈6.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】做大小两个长方体纸盒,尺寸如下(单位:cm)

(1)做这两个纸盒共用料多少cm2?
(2)做大纸盒比做小纸盒多用料多少cm2?
(3)如果a=8,b=6,c=5,将24个小纸盒包装成一个长方体,这个长方体的表面积的最小值为________cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.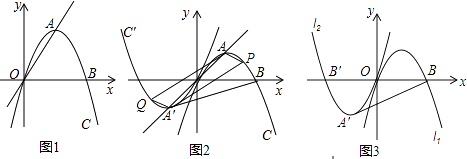
(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2 , l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2 , 请在第三象限内画出△A2B2C2 , 并求出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点. 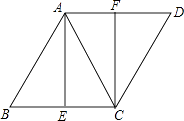
(1)求证:△ABE≌△CDF;
(2)若∠B=60°,AB=4,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列4个命题: ①方程x2﹣( ![]() +
+ ![]() )x+
)x+ ![]() =0的根是
=0的根是 ![]() 和
和 ![]() .
.
②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD= ![]() ,则CD=3.
,则CD=3.
③点P(x,y)的坐标x,y满足x2+y2+2x﹣2y+2=0,若点P也在y= ![]() 的图象上,则k=﹣1.
的图象上,则k=﹣1.
④若实数b、c满足1+b+c>0,1﹣b+c<0,则关于x的方程x2+bx+c=0一定有两个不相等的实数根,且较大的实数根x0满足﹣1<x0<1.
上述4个命题中,真命题的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水源村在今年退耕还林活动中,计划植树200亩,全村在完成植树40亩后,某环保组织加入村民植树活动,并且该环保组织植树的速度是全村植树速度的1.5倍,整个植树过程共用了13天完成.
(1)全村每天植树多少亩?
(2)如果全村植树每天需2000元工钱,环保组织是义务植树,因此实际工钱比计划节约多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com