
【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.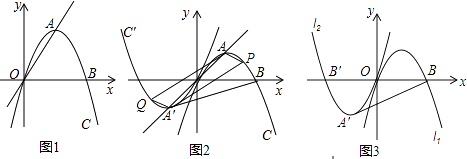
(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2 , l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由.
【答案】
(1)
解:如图1,
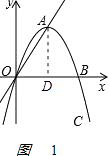
过A作AD⊥OB于D点,
∵抛物线l1:y=ax2+bx+c(a<0)过原点和B(4,0).
顶点为A.OD= ![]() OB=2.
OB=2.
又∵直线OA的解析式为y=x,
∴AD=OD=2.
∴点A的坐标为(2,2),
将A、B、O的坐标代入y=ax2+bx+c(a<0)中,
![]() ,
,
解得 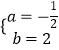 ,
,
∴抛物线C的解析式为y=﹣ ![]() x2+2x
x2+2x
(2)
解:如图2,
 ,
,
∵AO=A′O,PO=OQ,
∴四边形PAQA′是平行四边形,
∴S平行四边形PAQA′=4S△AOP.
过点P作PE⊥y轴于E交AO于F.
设P(x,﹣ ![]() x2+2x),则F(﹣
x2+2x),则F(﹣ ![]() x2+2x,﹣
x2+2x,﹣ ![]() x2+2x),
x2+2x),
若P点在抛物线AB段(2<x≤4)时,S△AOP= ![]() |xP﹣xF|×|yA|=
|xP﹣xF|×|yA|= ![]() [x﹣(﹣
[x﹣(﹣ ![]() x2+2x)]×2=
x2+2x)]×2= ![]() x2﹣x,
x2﹣x,
则S平行四边形PAQA′=4S△AOP=2x2﹣4x(2<x≤4)
(3)
解:如图3,
 ,
,
作A′B的垂直平分线l,分别交A′B、x轴于M、N(n,0),由旋转的性质,得l2的顶点坐标A′(﹣2,﹣2),
故A′B的中点M的坐标(1,﹣1).
作MT⊥x轴于T,在Rt△NMB中,MT⊥NB于T,
∠NMT+∠BMT=90°,∠TBM+∠BMT=90°,
∴∠NMT=∠TBM,
又∵∠NTM=∠BTM=90°,
∴△MTN∽△BTM,
![]() =
= ![]() ,
,
MT2=TNTB,即12=(1﹣n)(4﹣1).
∴n= ![]() ,即N点的坐标为(
,即N点的坐标为( ![]() ,0).
,0).
直线l过点M(1,﹣1)、N( ![]() ,0),
,0),
∴直线l的解析式为y=﹣3x﹣2.
解 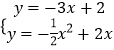 ,得x=5
,得x=5 ![]() .
.
在抛物线l1上存在两点使得HB=HA′,其坐标分别为(5+ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ),(5﹣
),(5﹣ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ).
).
解  得x=﹣5
得x=﹣5 ![]() ,在抛物线l2上存在两点使得HB=HA′,其坐标分别为(﹣5+
,在抛物线l2上存在两点使得HB=HA′,其坐标分别为(﹣5+ ![]() ,17﹣3
,17﹣3 ![]() ),(﹣5﹣
),(﹣5﹣ ![]() ,17+3
,17+3 ![]() );
);
综上所述:(5+ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ),(5﹣
),(5﹣ ![]() ,﹣13﹣3
,﹣13﹣3 ![]() ),(﹣5+
),(﹣5+ ![]() ,17﹣3
,17﹣3 ![]() ),(﹣5﹣
),(﹣5﹣ ![]() ,17+3
,17+3 ![]() )
)
【解析】(1)根据O、B关于对称轴对称,可得OD的长,根据A在直线y=x上,可得A点坐标,根据待定系数法,可得答案;(2)根据平行四边形的性质,可得S平行四边形PAQA′=4S△AOP , 根据平行于x轴的直线上两点间的距离是较大的横坐标减较小的横坐标,可得PF的长,根据三角形的面积,可得答案;(3)根据线段垂直平分线上的点到线段两端点的距离相等,可得H在线段A′B的垂直平分线上,根据解方程组,可得H点的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题: 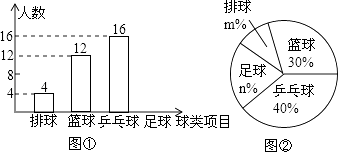
(1)九(1)班的学生人数为 , 并把条形统计图补充完整;
(2)扇形统计图中m= , n= , 表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE. 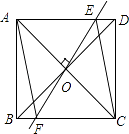
(1)求证:四边形AECF是菱形
(2)若AB=3,BC=4,则菱形AECF的周长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,P是线段AB上的任意一点,在AB的同侧分别以AP、PB为边作等边三角形APC和等边三角形PBD,连结CD.
(1)当AP=6时,求CD的长;
(2)当AP为多少时,CD的值最小,最小值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了 ![]() ,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
A.![]() =
= ![]() ×
× ![]()
B.![]() =
= ![]() ×
× ![]()
C.![]() +
+ ![]() =
= ![]()
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)分别写出以上三组数据的平均数、众数、中位数;
(2)这三个厂家的推销广告分别用了哪一种表示集中趋势的特征数?
(3)如果你是顾客,宜选购哪家工厂的产品?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x的图象与函数y= ![]() 的图象在第一象限内交于点B,点C是函数y=
的图象在第一象限内交于点B,点C是函数y= ![]() 在第一象限图象上的一个动点,当△OBC的面积为3时,点C的横坐标是 .
在第一象限图象上的一个动点,当△OBC的面积为3时,点C的横坐标是 . 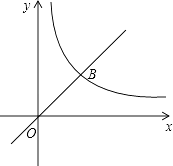
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com