
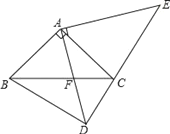
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连接BD.
(1)求证:BD=EC;
(2)BD与CE有何位置关系?请证你的猜想.
【答案】(1)证明见解析;(2) BD垂直于CE,理由见解析.
【解析】试题分析:(1)根据同角的余角相等得出∠BAD=∠CAE,结合已知条件得出△BAD和△CAE全等,从而得出答案;(2)根据全等得出∠ADB=∠AED,然后根据直角三角形的性质以及等量代换得出∠BDE=90°,从而得出垂直.
试题解析:(1)∵∠BAC=∠DAE=90°,∴∠BAD+∠CAD=∠CAE+∠CAD,
即∠BAD=∠CAE, ∵在△BAD和△CAE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE(SAS), ∴BD=CE;
(2)∵△BAD≌△CAE,∴∠ADB=∠AED, ∵∠ADE+∠AED=90°,
∴∠ADE+∠ADB=90°,即∠BDE=90°,则BD⊥CE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
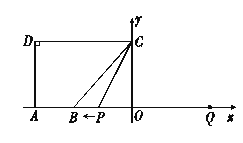
【题目】如图,![]() 点
点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为![]() 秒.
秒.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 随点
随点![]() 的运动而变化,当
的运动而变化,当![]() 与四边形
与四边形![]() 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.若收入10元,记作+10元,则-8元的意义是( )
A. 收入8元 B. 支出8元 C. 支出-8元 D. 收入2元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 0是绝对值最小的有理数
B. 一个有理数不是整数,就是分数
C. 任何一个有理数都能用数轴上的一个点来表示
D. 如果一个数的平方等于它本身,那么这个数是-1或0或1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
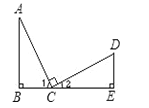
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】曲靖市的职业教育是曲靖市教育的一张名片,现在曲靖市中等职业学校在校生约为130000人,将数字130000用科学记数法表示为( )
A.0.13×105B.0.13×106C.1.3×105D.1.3×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com