
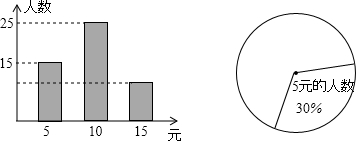
分析 (1)用捐款5元的人数除以它所占的百分比即可解答;
(2)用样本容量分别减去捐款5元的人数和捐款10元的人数得到捐款15元的人数,于是可计算出捐款15元的人数的百分比,然后用360°乘以这个百分比即可得到捐款15元的人数所占的圆心角的度数;
(3)先样本的平均数,根据样本估计总体,用800乘以这个平均数可估计出九年级学生捐款总数.
解答 解:(1)15÷30%=50(人),
答:本次抽样的学生有50人;
(2)捐款15元的人数=50-15-25=10(人),
360°×$\frac{10}{50}$=72°,
答:该样本中捐款15元的人数所占的圆心角度数为72°;
(3)据此信息可估计该校六年级学生每人捐款为:
(5×15+10×25+15×10)÷(15+25+10)
=720÷50
=9.5(元)
9.5×800=7600(元).
答:八年级捐款总数为7600元.
点评 本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.从条形图可以很容易看出数据的大小,便于比较.也考查了样本估计总体和扇形统计图.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:选择题
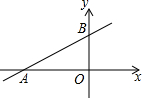 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
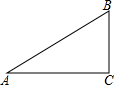 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )| A. | 45 | B. | 5 | C. | $\frac{1}{5}$ | D. | $\frac{1}{45}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
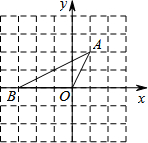 如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.
如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
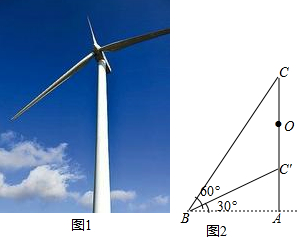
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
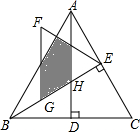 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{25}{40}$ | B. | $\frac{24}{41}$ | C. | $\frac{23}{40}$ | D. | $\frac{25}{41}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
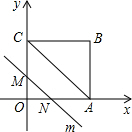 在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )| A. | 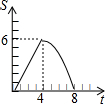 | B. | 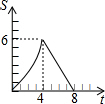 | C. | 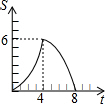 | D. | 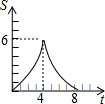 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com