
已知:如图,在△ABC中,AB=AC,∠BAC= ,且60°<
,且60°< <120°.P为△ABC内部一点,且PC=AC,∠PCA=120°—
<120°.P为△ABC内部一点,且PC=AC,∠PCA=120°— .
.
(1)用含 的代数式表示∠APC,得∠APC =_______________________;
的代数式表示∠APC,得∠APC =_______________________;
(2)求证:∠BAP=∠PCB;
(3)求∠PBC的度数.
(1)∠APC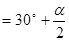 .
.
(2)证明:如图5. 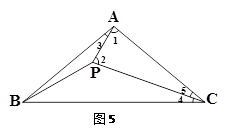
∵CA=CP,
∴∠1=∠2=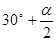 .
.
∴∠3=∠BAC-∠1=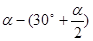 =
=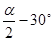 .
.
∵AB=AC,
∴∠ABC=∠ACB=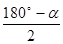 =
=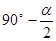 .
.
∴∠4=∠ACB-∠5=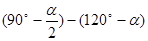 =
=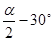 .
.
∴∠3=∠4.
即∠BAP=∠PCB.
(3)在CB上截取CM使CM=AP,连接PM(如图6).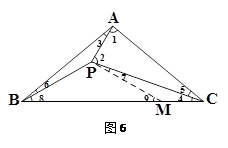
∵PC=AC,AB=AC,
∴PC=AB.
在△ABP和△CPM中,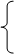 AB=CP,
AB=CP,
∠3=∠4,
AP=CM,
∴△ABP≌△CPM.
∴∠6=∠7, BP=PM.
∴∠8=∠9.
∵∠6=∠ABC-∠8,∠7=∠9-∠4,
∴∠ABC-∠8=∠9-∠4.
即(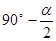 )-∠8=∠9-(
)-∠8=∠9-(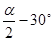 ).
).
∴ ∠8+∠9=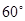 . ∴2∠8=
. ∴2∠8=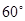 .
.
∴∠8=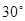 即∠PBC=
即∠PBC=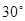 .
. 
解析


科目:初中数学 来源: 题型:
 (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com