
【题目】(1)已知 y y1 y2 ,而 y1与 x 1成正比例, y2与 x2 成正比例,并且x 1 时,y 2;x 0 时,y 2,求y与x的函数关系式;
(2)如图,直线 y 2 x 3 与 x 轴相交于点 A,与 y 轴相交于点 B.
①求 A、B 两点的坐标;
②过 B 点作直线 BP 与 x 轴相交于 P,且使 AP=2OA,求△BOP 的面积。

【答案】(1)y=-2x2+2x+2;
(2)①A(![]() ,0) B(0,3);
,0) B(0,3);
②![]() 或
或![]()
【解析】
(1)根据正比例的定义设出y与x之间的函数关系式,然后利用待定系数法求函数解析式即可得解;
(2)令y=0即可求出点A的横坐标,令x=0即可求出点B的纵坐标;
(3)分点P在点A的左侧和右侧两种情况求解即可.
解:(1)∵y1与x+1成正比例,y2与x2成正比例
设y1=a(x+1),y2=bx2,
∴y=a(x+1)+bx2,
∵x 1 时,y 2;x 0 时,y 2,
∴![]() ,
,
解得![]() ,
,
∴y=2(x+1)-2x2=-2x2+2x+2;
(2)①∵y=2x+3,
∴当y=0时,x=![]() ;当x=0时,y=3,
;当x=0时,y=3,
∴A(![]() ,0) B(0,3);
,0) B(0,3);
②当P在A左侧时,AP=2OA=3,OP=OA+AP=![]() ,
,
∴S△BOP=![]() ×3×
×3×![]() =
=![]() ;
;
当P在A右侧时,AP=2OA=3,OP=AP-OA=![]() ,
,
∴S△BOP=![]() ×3×
×3×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】为庆祝祖国70华诞,某小区计划在一块面积为196m2的正方形空地上建一个面积为100m2的长方形花坛(长方形的边与正方形空地的边平行),要求长方形的长是宽的2倍.请你通过计算说明该小区能否实现这个愿望?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF

(1)求证:∠E=∠C;
(2)如果DF平分∠AFB,求证:AC⊥AB
查看答案和解析>>
科目:初中数学 来源: 题型:
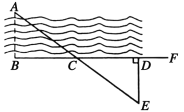
【题目】如图,是方城县潘河的某一段,现要测量河的宽度(即河两岸相对的两点A、B间的距离),先在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使点A、C、E在同一条直线上,直接在河岸上测量DE的长度就知道河的宽度AB了,你知道这是为什么吗?请先判断DE和AB大小关系,然后说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a2(﹣a4)+2(a2)3
(2)(2x﹣1)(2x+1)﹣(x﹣6)(4x+3)
(3)(2x﹣3y)2+2(y+3x)(3x﹣y)
(4)(a﹣2b+3)(a+2b+3)
(5) ![]()
(6)(2m+3n)(2m﹣n)﹣2n(2m﹣n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施,该设施的下部ABCD是矩形,其中AB=2米,BC=![]() 米,上部△CDG是等边三角形,固定点E为AB的中点。△EMN是由电脑控制其变化的三角通风窗(阴影部分均不通风),MN(MN可与CD重合)是可以沿设施边框上下滑动且始终保持与AB平行的伸缩横杆。(当MN在DC上方时,MD的长度是MN到DC距离的
米,上部△CDG是等边三角形,固定点E为AB的中点。△EMN是由电脑控制其变化的三角通风窗(阴影部分均不通风),MN(MN可与CD重合)是可以沿设施边框上下滑动且始终保持与AB平行的伸缩横杆。(当MN在DC上方时,MD的长度是MN到DC距离的![]() 倍)
倍)

(1)当MN和AB之间的距离为0.5米时,求此时 △EMN的面积;
(2)设MN与AB之间的距离为x米,求△EMN的面积S(平方米)与x的函数关系式;
(3)探究△EMN的面积S(平方米)有无最大值,若有,求出这个最大值;若无,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com