
分析 (1)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(2)原式先计算乘除运算,再计算加减运算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=8-(-4-9)÷(-3)=8-$\frac{13}{3}$=$\frac{11}{3}$;
(2)原式=(-16+9)÷$\frac{15}{8}$=-7×$\frac{8}{15}$=-$\frac{56}{15}$;
(3)原式=-(-$\frac{15}{4}$×4+$\frac{2}{5}$×$\frac{25}{4}$)×(-$\frac{3}{5}$)+16=-9+$\frac{3}{2}$+16=8$\frac{1}{2}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
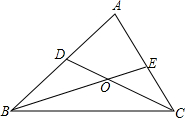 如图所示,在△ABC中,∠ABC和∠ACB的平分线BE和CD相交于点O.
如图所示,在△ABC中,∠ABC和∠ACB的平分线BE和CD相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
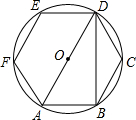 如图所示,正六边形ABCDEF内接于圆O,则cos∠ADB的值为( )
如图所示,正六边形ABCDEF内接于圆O,则cos∠ADB的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com