
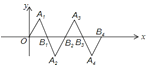
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是 。
【答案】(4n+1,![]() )
)
【解析】
试题分析:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,![]() ),B1的坐标为(2,0),
),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A2的坐标是(3,﹣![]() ),
),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣![]() )=
)=![]() ,
,
∴点A3的坐标是(5,![]() ),
),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A4的坐标是(7,﹣![]() ),
),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是![]() ,当n为偶数时,An的纵坐标是﹣
,当n为偶数时,An的纵坐标是﹣![]() ,
,
∴顶点A2n+1的纵坐标是![]() ,
,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,![]() ).
).


科目:初中数学 来源: 题型:
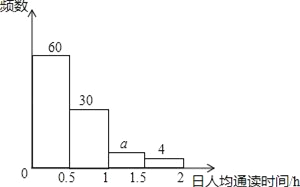
【题目】某校1200名学生参加了全区组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分.
根据以上信息,解答下列问题:
(1)本次调查的学生数为__人;
(2)图表中的a、b、c的值分别为__,__,__;
(3)在被调查的学生中,四月份日人均诵读时间在1<x≤1.5范围内的人数比三月份在此范围的人数多__人;
(4)试估计该校学生四月份人均诵读时间在1小时以上的人数.
四月日人均诵读时间的统计表
日人均诵读时间x/h | 人数 | 百分比 |
0≤x≤0.5 | 6 | |
0.5<x≤1 | 30 | |
1<x≤1.5 | 50% | |
1.5<x≤2 | 10 | 10% |
2<x≤2.5 | b | c |
三月日人均诵读时间的频数分布直方图
查看答案和解析>>
科目:初中数学 来源: 题型:
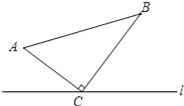
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=_________秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
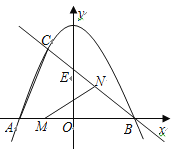
【题目】如图,抛物线![]() 与x轴交于点A、点B,与直线
与x轴交于点A、点B,与直线![]() 相交于点B、点C,直线
相交于点B、点C,直线![]() 与y轴交于点E。
与y轴交于点E。
(1)写出直线BC的解析式。
(2)求△ABC的面积。
(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A,B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒,请写出△MNB的面积S与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT 平分∠BAD交⊙O于点 T,过 T 作AD的垂线交 A D的延长线于点 C。
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=![]() ,求AD的长。
,求AD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+4x﹣5,设自变量的值分别为x1、x2、x3 , 且﹣1<x1<x2<x3 , 则对应的函数值y1、y2、y3的大小关系为( )
A.y1>y2>y3
B.y1<y2<y3
C.y2<y3<y1
D.y2>y3>y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com