
【题目】综合与探究
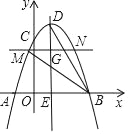
如图,抛物线y=﹣![]() x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
(1)求点A,B,D的坐标;
(2)点G为抛物线对称轴上的一个动点,从点D出发,沿直线DE以每秒2个单位长度的速度运动,过点C作x轴的平行线交抛物线于M,N两点(点M在点N的左边).
设点G的运动时间为ts.
①当t为何值时,以点M,N,B,E为顶点的四边形是平行四边形;
②连接BM,在点G运动的过程中,是否存在点M.使得∠MBD=∠EDB,若存在,求出点M的坐标;若不存在,请说明理由;
(3)点Q为坐标平面内一点,以线段MN为对角线作萎形MENQ,当菱形MENQ为正方形时,请直接写出t的值.
【答案】(1)A(﹣2,0),B(6,0);D(2,8);(2)①见解析;②存在,理由见解析;
(3)t=![]() .
.
【解析】分析:(1)令y=0,解方程﹣![]() x2+2x+6=0,即可求出A、B点的坐标,把y=﹣
x2+2x+6=0,即可求出A、B点的坐标,把y=﹣![]() x2+2x+6改写成顶点式,根据二次函数的性质求出D点的坐标;
x2+2x+6改写成顶点式,根据二次函数的性质求出D点的坐标;
(2)①要使四边形MEBN为平行四边形,则MN=BE=4,根据二次函数的对称性求出点M的坐标,从而求出DG的长,由DG=2t可求出t的值;②设BM交DE于P,如图,设P(2,m),在Rt△BEP中,根据PE2+BE2=PB2,列方程求出m的值,用待定系数法求出直线BP的解析式,与二次函数解析式联立,可求出点M的坐标;
(3)由正方形的性质得GN=GE=8﹣2t,从而表示出点N的坐标,把点N的坐标代入二次函数解析式求出t的值.
详解:(1)当y=0时,﹣![]() x2+2x+6=0,解得x1=﹣2,x2=6,则A(﹣2,0),B(6,0);
x2+2x+6=0,解得x1=﹣2,x2=6,则A(﹣2,0),B(6,0);
∵y=﹣![]() (x﹣2)2+8,
(x﹣2)2+8,
∴D(2,8);
(2)①∵E(2,0),B(6,0),
∴BE=4,
∵四边形MEBN为平行四边形,
∴MN=BE=4,
∵MN∥x轴,
∴MG=NG=2,
∴M点的横坐标为0,此时M(0,6)
∴2t=8﹣6,解得t=1,
∴当t为1s时,以点M,N,B,E为顶点的四边形是平行四边形;
②存在.
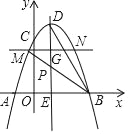
设BM交DE于P,如图,设P(2,m)
∵∠MBD=∠EDB,
∴PD=PB=8﹣m,
在Rt△BEP中,∵PE2+BE2=PB2,
∴m2+42=(8﹣m)2,解得m=5,
∴P(2,3),
设直线BP的解析式为y=px+q,
把B(6,0),P(2,3)代入得![]() ,解得
,解得![]() ,
,
∴直线BP的解析式为y=﹣![]() x+
x+![]() ,
,
解方程组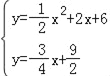 得
得![]() 或
或![]() ,
,
∴M点的坐标为(﹣![]() ,
,![]() );
);
(3)GE=8﹣2t,
∵菱形MENQ为正方形时,
∴GN=GE=8﹣2t,
∴N(10﹣2t,8﹣2t),
把N(10﹣2t,8﹣2t)代入y=﹣![]() x2+2x+6得﹣
x2+2x+6得﹣![]() (10﹣2t)2+2(10﹣2t)+6=8﹣2t,
(10﹣2t)2+2(10﹣2t)+6=8﹣2t,
整理得t2﹣9t+16,
∴t=![]() .
.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】中华文化,源远流长.在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
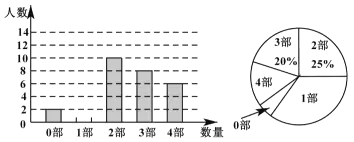
(1) 本次调查一共抽取了______名学生;扇形统计图中“1部”所在扇形的圆心角为______度
(2) 若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?
(3) 没有读过四大名著的两名学生准备从四大古典名著中各自随机选择一部来阅读,则他们选中同一名著的概率为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发向右运动,运动时间为t秒.

(1)若运动2秒时,则点P表示的数为_______,点P、Q之间的距离是______个单位;
(2)求经过多少秒后,点P、Q重合?
(3)试探究:经过多少秒后,点P、Q两点间的距离为6个单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小莉的爸爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用数状图或列表的方法求小莉去上海看世博会的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套房子,他准备将地面都铺上地砖,地面结构如图所示,请根据图中的数据(单位:米),解答下列问题:
(1)用含x,y的代数式表示地面总面积为 平方米;
(2)若x=5,y=1,铺地砖每平方米的平均费用为100元,则铺地砖的总费用为 元;
(3)已知房屋的高度为3米,现需要在客厅和卧室的墙壁上贴壁纸,那么用含x的代数式表示至少需要 平方米的壁纸;如果所粘壁纸的价格是100元/平方米,那么用含x的代数式表示购买该壁纸至少需要 元.(计算时不扣除门,窗所占的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数![]() ,可以组成两个有理数对
,可以组成两个有理数对![]() 与
与![]() .
.
我们规定:![]() .
.
例如:![]() .
.
根据上述规定解决下列问题:
(1)有理数对![]() ;
;
(2)若有理数对![]() ,则
,则![]() ;
;
(3)当满足等式![]() 的
的![]() 是整数时,求整数
是整数时,求整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EB.若AB=8,CD=2.
(1) 求⊙O半径OA的长;
(2) 求EB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com