
����Ŀ��С��������һ���ӣ����������涼���ϵ�ש������ṹ��ͼ��ʾ�������ͼ�е����ݣ���λ���ף�������������⣺
��1���ú�x��y�Ĵ���ʽ��ʾ���������Ϊ�� ��ƽ���ף�
��2����x��5��y��1���̵�שÿƽ����ƽ������Ϊ100Ԫ�����̵�ש���ܷ���Ϊ�� ��Ԫ��
��3����֪���ݵĸ߶�Ϊ3�ף�����Ҫ�ڿ��������ҵ�ǽ��������ֽ����ô�ú�x�Ĵ���ʽ��ʾ������Ҫ�� ��ƽ���ı�ֽ�������ճ��ֽ�ļ۸���100Ԫ/ƽ���ף���ô�ú�x�Ĵ���ʽ��ʾ����ñ�ֽ������Ҫ�� ��Ԫ��������ʱ���۳��ţ�����ռ�������

���𰸡���1����6x+2y+18������2��5000����3����78+6x������7800+600x����
��������
��1����������������ĸ����־��ε����֮����ʽ�������ɵý⣻
��2����x��5��y��1������ô𰸼��ɣ�
��3���ȸ��ݳ����ε������ʽ���������ֽ�������Ȼ���ñ�ֽ�ļ۸����������ɵó�������ã�
�⣺��1�����������Ϊ��6x+2��(6��3)+2y+3��(2+2)��
��6x+6+2y+12
��(6x+2y+18) ƽ���ף�
��2����x��5��y��1����1ƽ����ש��ƽ������Ϊ100Ԫʱ��
�ܷ��ã�(6��5+2��1+18)��100��50��100��5000Ԫ��
���̵�ש���ܷ���Ϊ5000Ԫ��
��3����������ã�3��3��2+4��3��2+6��3��2+3x��2=(78+6x) ƽ���ף�
(78+6x) ��100=(7800+600x)Ԫ��
���ڿ��������ҵ�ǽ��������ֽ����ô������Ҫ(78+6x)ƽ���ı�ֽ��������Ҫ(7800+600x)Ԫ��
�ʴ�Ϊ����1��(6x+2y+18)����2��5000����3��(78+6x)��(7800+600x)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[���ⱳ��]![]() ���ߵij��ֱ�Ϊ
���ߵij��ֱ�Ϊ![]() ,����������ε������
,���������������
С��ͬѧ�ڽ������ʱ���Ƚ���һ������������(ÿ��С�����εı߳�Ϊ![]() )�������������������
)�������������������![]() (��
(��![]() �������㶼��С�����εĶ��㴦),��ͼ1��ʾ����������Ҫ��
�������㶼��С�����εĶ��㴦),��ͼ1��ʾ����������Ҫ��![]() �ĸߣ�����������ܼ����
�ĸߣ�����������ܼ����![]() �����Ϊ_ ��
�����Ϊ_ ��
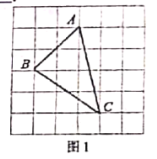
[˼ά��չ]���ǰ�������![]() ����ķ���������ͼ������
����ķ���������ͼ������![]() ���ߵij��ֱ�Ϊ
���ߵij��ֱ�Ϊ![]() ,������ͼ2������������(ÿ��С�����εı߳�Ϊ
,������ͼ2������������(ÿ��С�����εı߳�Ϊ![]() )������Ӧ��
)������Ӧ��![]() ��������������:
��������������:
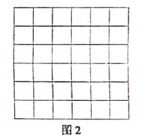
[̽������]��![]() ���ߵij��ֱ�Ϊ
���ߵij��ֱ�Ϊ![]() (����
(����![]() ��
��![]() ),�����ù�ͼ�������������ε����(����ͼ�β��������)��
),�����ù�ͼ�������������ε����(����ͼ�β��������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������A�س���������ʻ��B�أ��׳���80km/h���ٶ���ʻ1h���ҳ�������ͬ·����ʻ���ҳ��ȵ���B�ز�ͣ��1h������ԭ�ٰ�ԭ·���أ�ֱ����׳��������ڴ˹����У�����֮��ľ���y��km�����ҳ���ʻʱ��x��h��֮��ĺ�����ϵ��ͼ��ʾ������˵�������ҳ����ٶ���120km/h����m=160������H�������ǣ�7��80������n=7.5��
����˵����ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����ȡ����ѧ�����͡�ѧϰϰ�ߡ����е��飬�������Լ���������Ŀ���������������������� (ѡ��Ϊ�����١���ʱ������������)�ĵ������ݽ��������������Ƴɲ���ͳ��ͼ���£�

�����ͼ����Ϣ������������⣺
��1���õ������������Ϊ_______��![]() ________ ����
________ ����![]() ________�������١���Ӧ���ε�Բ�Ľ�Ϊ_____________��
________�������١���Ӧ���ε�Բ�Ľ�Ϊ_____________��
��2���벹ȫ����ͳ��ͼ��
��3������У����3500��ѧ��������������С����ǡ��Դ������������������������ѧ���ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
��ͼ��������y=��![]() x2+2x+6��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����Գ����������߽��ڵ�D����x�ύ�ڵ�E��
x2+2x+6��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����Գ����������߽��ڵ�D����x�ύ�ڵ�E��
��1�����A��B��D�����ꣻ
��2����GΪ�����߶Գ����ϵ�һ�����㣬�ӵ�D��������ֱ��DE��ÿ��2����λ���ȵ��ٶ��˶�������C��x���ƽ���߽���������M��N���㣨��M�ڵ�N����ߣ���
���G���˶�ʱ��Ϊts��
�ٵ�tΪ��ֵʱ���Ե�M��N��B��EΪ������ı�����ƽ���ı��Σ�
������BM���ڵ�G�˶��Ĺ����У��Ƿ���ڵ�M��ʹ�á�MBD=��EDB�������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����QΪ����ƽ����һ�㣬���߶�MNΪ�Խ�����ή��MENQ��������MENQΪ������ʱ����ֱ��д��t��ֵ��
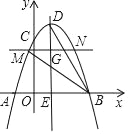
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��O��B������ͬһֱ���ϣ�OE��OD�ֱ�ƽ�֡�AOC����BOC��
��1�����EOD�Ķ�����
��2������AOE��50�������BOC�Ķ�����
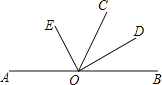
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����һ�����֣�Ȼ��ش��������⣮
��֪��ƽ����������![]() ��
��![]() ���������ľ���
���������ľ���![]() ��ͬʱ�����������ڵ�ֱ�����������ƽ�����������ֱ��������ʱ���������빫ʽ�ɻ���Ϊ
��ͬʱ�����������ڵ�ֱ�����������ƽ�����������ֱ��������ʱ���������빫ʽ�ɻ���Ϊ![]() ��
��![]()
![]() .
.
��1����֪![]() ��
��![]() ������A��B�����ľ���______.
������A��B�����ľ���______.
��֪M��N��ƽ����y���ֱ���ϣ���M��������Ϊ4����N��������Ϊ-1������M��N����ľ���Ϊ______��
��2����֪һ�������θ���������Ϊ![]() ��
��![]() ��
��![]() �������ж��������ε���״��?˵�����ɣ�
�������ж��������ε���״��?˵�����ɣ�
��3���ڣ�2���������£�ƽ��ֱ������ϵ�У���x������һ��P��ʹ![]() �ij�����̣������P�����꼰
�ij�����̣������P�����꼰![]() ����̳��ȣ�
����̳��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A��90�㣬��D��E�ֱ���AC��BC�ϣ���CD��BC��AC��CE����EΪԲ�ģ�DE��Ϊ�뾶��Բ����E������B����AB��BC�ֱ��ڵ�F��G��
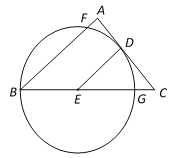
��1����֤��AC�ǡ�E�����ߣ�
��2����AF��4��CG��5�����E�İ뾶��
��3����Rt��ABC������ԲԲ��ΪI�����I�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��������ƽ��ÿ����۳�20����ÿ��ӯ��40Ԫ��Ϊ���������ۣ�����ӯ���� ������ٿ�����̳�������ȡ�ʵ��Ľ��۴�ʩ��������һ����Χ�ڣ������ĵ���ÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�2����������ĵ��۽���xԪ��
��1�����̳����ۺ�ÿ��ӯ��___________Ԫ��ÿ����۳�________����
��2������̳�ͨ��������������ÿ��ӯ��1200Ԫ����ô�����ĵ��۽��˶���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com