
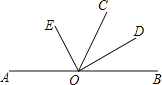
【题目】已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.
【答案】(1)90°;(2)80°
【解析】
(1)由于OE、OD分别平分∠AOC、∠BOC,所以∠EOC=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,进而得出∠EOD=∠EOC+∠COD=
∠BOC,进而得出∠EOD=∠EOC+∠COD=![]() ∠AOB=90°;
∠AOB=90°;
(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°﹣∠AOC=80°.
(1)∵OE、OD分别平分∠AOC、∠BOC,
∴∠EOC=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,
∠BOC,
∴∠EOD=∠EOC+∠COD=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() ∠AOB,
∠AOB,
又∵A、O、B三点在同一直线上,
∴∠AOB=180°,
∴∠EOD=![]() ∠AOB=90°;
∠AOB=90°;
(2)∵OE平分∠AOC,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
∴∠BOC=180°﹣∠AOC=80°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校七年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
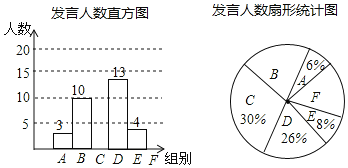
(1)直接写出随机抽取学生的人数为 人;
(2)直接补全频数直方图和扇形统计图;
(3)该校七年级共有学生1000人,请估计七年级在这天里发言次数大于等于12次的人数.
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套房子,他准备将地面都铺上地砖,地面结构如图所示,请根据图中的数据(单位:米),解答下列问题:
(1)用含x,y的代数式表示地面总面积为 平方米;
(2)若x=5,y=1,铺地砖每平方米的平均费用为100元,则铺地砖的总费用为 元;
(3)已知房屋的高度为3米,现需要在客厅和卧室的墙壁上贴壁纸,那么用含x的代数式表示至少需要 平方米的壁纸;如果所粘壁纸的价格是100元/平方米,那么用含x的代数式表示购买该壁纸至少需要 元.(计算时不扣除门,窗所占的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的原点为0,点A、B、C是数轴上的三点,点B对应的数位1,AB=6,BC=2,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0)
(1)求点A、C分别对应的数;
(2)经过t秒后,求点P、Q分别对应的数(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组连续奇数按如图方式排列,请你解决下列问题:

![]() 第
第![]() 行最后一个数字是___________,在第
行最后一个数字是___________,在第![]() 行第
行第![]() 列的数字是_______________
列的数字是_______________
![]() 请用含
请用含![]() 的代数式表示第
的代数式表示第![]() 行的第
行的第![]() 个数字和最后一个数字;
个数字和最后一个数字;
![]() 现用一个正方形框去围出相邻两行中的
现用一个正方形框去围出相邻两行中的![]() 个数字(例如:第
个数字(例如:第![]() 行和第
行和第![]() 行的
行的![]() ),请问能否在第
),请问能否在第![]() 行和第
行和第![]() 行中求出
行中求出![]() 个数字的和是
个数字的和是![]() ?若能,请求出这
?若能,请求出这![]() 个数字;若不能,请说明理由.
个数字;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
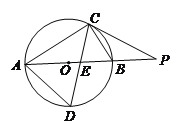
【题目】如图,⊙O的直径AB为2cm,弦BC为1cm,∠ACB的平分线与⊙O交于点D,与AB交于点E,P为AB延长线上一点,连接PC,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com