
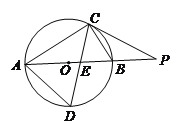
【题目】如图,⊙O的直径AB为2cm,弦BC为1cm,∠ACB的平分线与⊙O交于点D,与AB交于点E,P为AB延长线上一点,连接PC,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
【答案】(1)AC=![]() cm,AD=
cm,AD=![]() ;(2) 直线PC与⊙O相切,理由见解析
;(2) 直线PC与⊙O相切,理由见解析
【解析】(1)连接BD,如图,根据圆周角定理由AB为直径得∠ACB=∠ADB=90°,则可利用勾股定理计算出![]() 由CD平分∠ACB得
由CD平分∠ACB得![]() 根据圆周角定理得
根据圆周角定理得![]() 则
则![]() 为等腰直角三角形,由勾股定理即可得出
为等腰直角三角形,由勾股定理即可得出![]() 的长;
的长;
(2)连接OC,由PC=PE,得∠PCE=∠PEC,利用三角形外角性质得∠PEC=∠CAE+∠ACE,根据CD平分∠ACB,得到∠ACE=∠ECB,∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,于是根据切线的判定定理可得PC为![]() 的切线.
的切线.
(1)①如图,连接BD,
∵AB是直径,
∴∠ACB=∠ADB=90°,
在![]() 中,
中,
AC=![]() =
=![]() =
= ![]() cm,
cm,
②∵CD平分∠ACB,
![]()
![]()
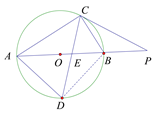
∴AD=BD,
∴Rt△ABD是直角等腰三角形,
![]()
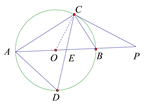
(2)直线PC与⊙O相切,
理由:连接OC,
∵OC=OA,
∴∠CAO=∠OCA,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE,
∵CD平分∠ACB,
∴∠ACE=∠ECB,
∴∠PCB=∠ACO,
∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠CB=90°,
OC⊥PC,
∴直线PC与⊙O相切.


科目:初中数学 来源: 题型:
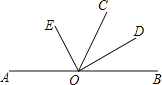
【题目】已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;①AD平分∠BAC;③AE=AD;④AB+AC=2AE.其中正确的有( ).
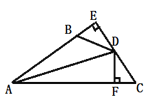
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
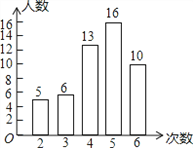
【题目】我市开展了“寻找雷锋足迹”的活动,某中学为了解七年级1000名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
(1)所调查的七年级50名学生在这个月内做好事次数的平均数是 ,众数是 ,中位数是 ;
(2)根据样本数据,估计该校七年级1000名学生在“学雷锋活动月”中做好事大于4次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利, 尽快减少库存,商场决定采取适当的降价措施.假设在一定范围内,衬衫的单价每降低1元,商场平均每天可多售出2件.设衬衫的单价降了x元:
(1)该商场降价后每件盈利___________元,每天可售出________件;
(2)如果商场通过销售这批衬衫每天盈利1200元,那么衬衫的单价降了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.
(1)当矩形EFPQ为正方形时,求正方形的边长;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线BC匀速向右运动(当矩形的顶点Q到达C点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行了有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会. 在一个纸盒里装有2个红求和2个白球,除颜色外其他都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表)
甲 超 市
球 | 两红 | 一红一白 | 两白 |
礼金券 | 5 | 10 | 5 |
乙 超 市
球 | 两红 | 一红一白 | 两白 |
礼金券 | 10 | 5 | 10 |
(1)用树状图或列表法表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.
如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.
若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……
△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn,则点A1的坐标是__,点A2018的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com